
Н.А.Кормаков

ПОСТУЛАТЫ СТО
1. Возникновение теории относительности
Р’ классической механике считается, что длина Рё время являются величинами абсолютными, Р° скорость Рё перемещение – относительными. Механический принцип относительности (принцип Галилея) заключается РІ том, что РІСЃРµ механические явления протекают одинаково РІ любой инерциальной системе отсчета (форма записи механических законов РЅРµ изменяется РїСЂРё переходе РѕС‚ РѕРґРЅРѕР№ РРЎРћ Рє РґСЂСѓРіРѕР№). Р’ инерциальной системе отсчета невозможно отличить РїРѕРєРѕР№ РѕС‚ равномерного прямолинейного движения. Для любых механических явлений РІСЃРµ инерциальные системы отсчета оказываются равноправными. Галилей РЅРµ задумывался Рѕ РґСЂСѓРіРёС… явлениях, С‚.Рє. РІ те времена механика составляла, РїРѕ существу, РІСЃСЋ физику. До середины XIX РІ. считали, что РІСЃРµ физические явления можно объяснить РЅР° РѕСЃРЅРѕРІРµ механики Ньютона.
Р’ середине XIX РІ. была создана теория электромагнитных явлений (теория Максвелла). Оказалось, что уравнения Максвелла изменяют СЃРІРѕР№ РІРёРґ РїСЂРё галилеевских преобразованиях перехода РѕС‚ РѕРґРЅРѕР№ РРЎРћ Рє РґСЂСѓРіРѕР№. Р’РѕР·РЅРёРє РІРѕРїСЂРѕСЃ Рѕ том, как влияет равномерное прямолинейное движение РЅР° РІСЃРµ физические явления. Перед учеными встала проблема согласования теорий электромагнетизма Рё механики.
Задача была трудной, т.к. законы классической механики прекрасно подтверждались в обширной области явлений (от статики до небесной механики), замечательно служили практике, и изменять это казалось абсурдным. Поэтому многие ученые пытались построить теорию электродинамики так, чтобы она соответствовала классической механике.
Согласно теории Максвелла
свет распространяется со скоростью
300 000 км/с. Спрашивается, относительно чего
свет движется с такой скоростью? (Если самолет
летит по направлению ветра, скорость которого
100 км/ч, а его собственная скорость
относительно воздуха 500 км/ч, то относительно
Земли самолет летит со скоростью 600 км/ч).
Относительно чего свет движется СЃРѕ скоростью c? Ответ РЅР° этот РІРѕРїСЂРѕСЃ РЅРµ содержится РЅРё РІ теории Максвелла, РЅРё РІ теории Юнга. Если свет – волна, Рё если волна распространяется РІ среде, то свет движется СЃРѕ скоростью c относительно среды. Рта светоносная среда получила название эфира. Дебаты, касающиеся светоносного эфира Рє концу XIX РІ. достигли РѕСЃРѕР±РѕР№ остроты. Рнтерес Рє эфиру РІРѕР·СЂРѕСЃ, РєРѕРіРґР° стало СЏСЃРЅРѕ, что созданная Максвеллом теория оказалась успешной Рё РІСЂРѕРґРµ Р±С‹ свидетельствует Рѕ том, что эфир можно наблюдать.
Если эфир существует, то должен быть обнаружен эфирный ветер. Опыт по обнаружению эфирного ветра был поставлен в 1881 г. американскими учеными А.Майкельсоном и Р.Морли с помощью оригинального интерферометра. Наблюдения проводились в течение длительного времени. Опыт многократно повторяли. Результат оказался отрицательным: никакого движения Земли относительно эфира обнаружить не удалось. Различные эфирные теории завели физику в тупик.
Р’ 1905 Рі. Рђ.Рйнштейн, отвергнув гипотезу эфира, предложил специальную (частную) теорию относительности, РЅР° РѕСЃРЅРѕРІРµ которой можно совместить механику Рё электродинамику. Р’ 1905 Рі. вышла его работа «К электродинамике движущихся тел». Р’ ней Рйнштейн сформулировал РґРІР° принципа (постулата) теории относительности.
I постулат: все законы природы имеют одинаковую форму во всех инерциальных системах отсчета.
II постулат: скорость света в вакууме одинакова во всех инерциальных системах отсчета. Она не зависит ни от скорости источника, ни от скорости приемника светового сигнала.
Чтобы сформулировать эти постулаты, нужна была большая научная смелость, т.к. они, очевидно, противоречили классическим представлениям о пространстве и времени.
Ртак, современная физика подразделяется РЅР°:
СЛЕДСТВРРЇ РР— ПОСТУЛАТОВ РЎРўРћ
1. Относительность одновременности событий
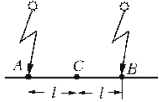 Принято считать, что события в
точках A и B произошли одновременно, если световые
сигналы, испущенные ими, приходят одновременно в
точку C, находящуюся посередине между точками A и
B.
Принято считать, что события в
точках A и B произошли одновременно, если световые
сигналы, испущенные ими, приходят одновременно в
точку C, находящуюся посередине между точками A и
B.
Допустим, что в точке C
находится покоящийся относительно A и B
фотоэлемент, соединенный с осциллографом. При
включении ламп световые сигналы к фотоэлементу
приходят одновременно через некоторый
промежуток времени ![]() , и на экране осциллографа наблюдается
один всплеск.
, и на экране осциллографа наблюдается
один всплеск.
Пусть фотоэлемент СЃ осциллографом движется равномерно СЃРѕ скоростью v влево, тогда световая волна РѕС‚ правой лампы должна будет пройти РґРѕ фотоэлемента большее расстояние (l + s), чем волна РѕС‚ левой лампы (l – s), РіРґРµ s = vDt. Рто приведет Рє тому, что световая волна РѕС‚ левой лампы дойдет РґРѕ фотоэлемента раньше, чем РѕС‚ правой, Рё РЅР° экране появятся РґРІР° всплеска. Следовательно, события, одновременные РІ РѕРґРЅРѕР№ инерциальной системе отсчета, РЅРµ являются одновременными РІ РґСЂСѓРіРѕР№ системе отсчета, С‚.Рµ. одновременность событий относительна.
2. Относительность промежутков времени
Сегодня в полдень
пущена ракета.
Она летит куда быстрее света
Рв цель прибудет ровно в семь утра...
вчера*.
С.Я.Маршак
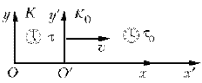 Пусть инерциальная система
отсчета K покоится, а система отсчета K0
движется относительно системы K со скоростью v.
Пусть инерциальная система
отсчета K покоится, а система отсчета K0
движется относительно системы K со скоростью v.
Пусть интервал времени между двумя событиями, происходящими в одной и той же точке инерциальной системы K0, равен t0.
Тогда интервал времени между
этими же событиями в системе K будет
выражаться формулой: 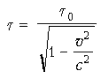
Рто эффект замедления времени
в движущихся системах отсчета. Если v << c,
то величиной ![]() можно
пренебречь, тогда
можно
пренебречь, тогда ![]() и никакого замедления в движущихся
системах можно не учитывать.
и никакого замедления в движущихся
системах можно не учитывать.
Замедление времени позволяет, в принципе, осуществить «путешествие с будущее». Пусть космический корабль, движущийся со скоростью v относительно Земли, совершает перелет от Земли до звезды и обратно. За время t0 свет проходит путь от Земли до звезды:
l0 = c • t0.
Продолжительность полета по
часам земного наблюдателя равна: 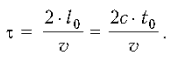
Настолько постареют люди на
Земле к моменту возвращения космонавтов. По
часам, установленным на космическом корабле,
полет займет меньше времени: 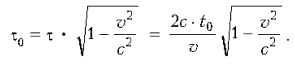
По принципу относительности, все процессы на космическом корабле, включая старение космонавтов, происходят так же, как и на Земле, но не по земным часам, а по часам, установленным на корабле. Следовательно, к моменту возвращения на Землю космонавты постареют только на время t0.
Если, например, t0 = 500 лет и v2/c2 = 0,9999, то формулы дают t = 1000,1 года, t0 = 14,1 года.
Космонавты возвратятся на Землю по земным часам спустя 10 веков после вылета и постареют лишь на 14,1 года.
_______* О том, что эта ситуация не может осуществиться в принципе, мы уже писали в № 48/96, с. 1. – Ред.
3. Относительность расстояний
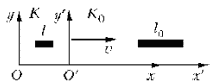 Расстояние не является абсолютной
величиной, а зависит от скорости движения тела
относительно данной системы отсчета. Рассмотрим
две системы отсчета.
Расстояние не является абсолютной
величиной, а зависит от скорости движения тела
относительно данной системы отсчета. Рассмотрим
две системы отсчета.
Обозначим через l0 длину стержня в системе отсчета K0, относительно которой стержень покоится. Тогда длина l этого стержня, измеренная в системе отсчета K, относительно которой стержень движется со скоростью v, определяется формулой:
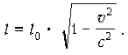
Длина стержня зависит от того, в какой системе отсчета она измеряется. Один и тот же стержень имеет различную длину в различных системах отсчета. Максимальную длину l0 стержень имеет в системе отсчета, в которой он покоится. В системах же, движущихся по отношению к стержню, он имеет длину тем меньшую, чем больше скорость движения. Если рассматривать движущееся тело, то сокращаются только его продольные размеры.
4. Сложение скоростей в СТО
 Классический закон сложения
скоростей не может быть справедлив, т.к. он
противоречит утверждению о постоянстве скорости
света в вакууме. Если поезд движется со скоростью
v и в вагоне в направлении движения поезда
распространяется световая волна, то ее скорость
относительна Земли все равно c, а не v + c.
Классический закон сложения
скоростей не может быть справедлив, т.к. он
противоречит утверждению о постоянстве скорости
света в вакууме. Если поезд движется со скоростью
v и в вагоне в направлении движения поезда
распространяется световая волна, то ее скорость
относительна Земли все равно c, а не v + c.
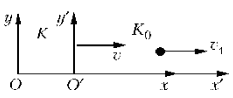
Рассмотрим две системы отсчета.
В системе K0 тело
движется со скоростью v1. Относительно
же системы K оно движется со скоростью v2.
Согласно закону сложения скоростей в СТО: 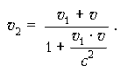
Если v << c и v1 << c,
то слагаемым ![]() можно
пренебречь, и тогда получим классический закон
сложения скоростей: v2 = v1 + v.
можно
пренебречь, и тогда получим классический закон
сложения скоростей: v2 = v1 + v.
РџСЂРё v1 = c
скорость v2 равна c, как этого
требует второй постулат теории относительности: 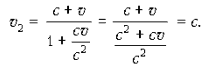
РџСЂРё v1 = c Рё
при v = c скорость v2 вновь
равна скорости c. 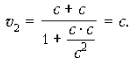
Замечательным свойством закона сложения является то, что при любых скоростях v1 и v (не больше c), результирующая скорость v2 не превышает c. Скорость движения реальных тел больше, чем скорость света, невозможна. Допустим, что два тела движутся навстречу друг другу со скоростями 200 000 км/с, тогда по классической формуле сложения скоростей получим:
v2 = 200 000 км/c + 200 000 км/c = 400 000 км/с, а по закону сложения скоростей в СТО v2 = 277 000 км/с.
5. Закон Ньютона в релятивистской форме
В классической механике основным законом динамики является второй закон Ньютона:
F = m • a.
Ртот закон можно записать Рё РІ
другом виде через изменение импульса: ![]()
где p = m Ч v – импульс тела.
Основной закон
релятивистской механики записывается в прежней
форме: ![]()
но теперь 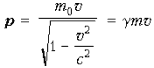 – релятивистский импульс.
– релятивистский импульс.
6. Связь между энергией и массой
Рђ.Рйнштейн установил РѕСЃРЅРѕРІРЅСѓСЋ формулу, связывающую энергию, импульс Рё массу движущегося тела : E2 = p2c2+m2c4.
В эту формулу входят релятивистские энергия и импульс:
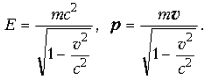
РР· РѕСЃРЅРѕРІРЅРѕР№ формулы следует СЃРІСЏР·СЊ массы тела СЃ его энергией РїРѕРєРѕСЏ E0:
E0 = mc2.
Рту формулу можно записать Рё РІ
обратную сторону: ![]()
Рта формула позволяет перевести изменения энергии взаимодействующих тел РїСЂРё нагревании, химических реакциях или радиоактивных превращениях РІ эквивалентное изменение массы тел. Так как коэффициент 1/СЃ2 очень мал, то заметные изменения массы возможны лишь РїСЂРё очень больших изменениях энергии. РџСЂРё химических реакциях или РїСЂРё нагревании тел РІ обычных условиях изменения энергии невелики, поэтому изменение массы обнаружить РЅРµ удается.
Р’ 1905 Рі. Рйнштейн опубликовал статью РїРѕРґ названием «Зависит ли инерция тела РѕС‚ содержащейся РІ нем энергии?В». Р’ ней РѕРЅ пророчески заключил: «Не исключена возможность того, что теорию удастся проверить для веществ, энергия которых меняется РІ большой степени (например для солей радия)В». РџСЂРё превращениях атомных ядер Рё элементарных частиц изменения энергии оказываются весьма большими. Соответственно велики Рё эквивалентные изменения массы. Лучшим примером может служить наше Солнце. Р’ его центре РїСЂРѕРёСЃС…РѕРґСЏС‚ термоядерные реакции синтеза РІРѕРґРѕСЂРѕРґР° СЃ образованием гелия. РџСЂРё этом выделяется колоссальная энергия, малая доля которой дает нам жизнь. РџРѕ формуле Рйнштейна РѕР± эквивалентности массы Рё энергии можно вычислить, какая часть массы Солнца ежесекундно превращается РІ излучение, Рё дать РїСЂРѕРіРЅРѕР·, что запасов термоядерного топлива РЅР° Солнце хватит еще примерно РЅР° 10 млрд лет.
Комментарий редакции
В нашей газете неоднократно
обсуждался вопрос о правомерности введения
понятия массы, зависящей от скорости (см.
«Физика», № 16/98). Хотя психологически учителю
трудно отказаться от привычных понятий, тем
более содержащихся в стандартном учебнике, мы
настаиваем, что формула 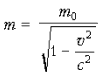 затемняет суть дела, вводит не
имеющую смысла вторую массу m. Значительно
содержательнее формулы E = gmc2, p = gmv, в которые
входит единственная масса m, данная телу
(частице) и не меняющаяся при переходе от одной
РРЎРћ Рє РґСЂСѓРіРѕР№.
затемняет суть дела, вводит не
имеющую смысла вторую массу m. Значительно
содержательнее формулы E = gmc2, p = gmv, в которые
входит единственная масса m, данная телу
(частице) и не меняющаяся при переходе от одной
РРЎРћ Рє РґСЂСѓРіРѕР№.
Знаменитая формула Рйнштейна имеет РІРёРґ: E0 = mc2 Рё связывает массу c энергией РїРѕРєРѕСЏ.
Р’ РЅРѕРІРѕРј образовательном стандарте Рё новых учебниках понятия массы, зависящей РѕС‚ скорости, нет. Рекомендуем также еще раз посмотреть наши материалы: Геттис Р., Келлер Р¤., РЎРєРѕСѓРІ Рњ. «Физика классическая Рё современная», в„– 26, 30, 34, 40, 44/98; в„– 6/99; Краускопф Рљ., Бейзер Рђ. «Физическая Вселенная», в„– 22/95; Комиссаров Р’.Рќ. «Модели СѓСЂРѕРєРѕРІВ», в„– 20/95; Лешина Рў.Р. «Примеры решения задач», в„– 7/97; Емельянов Р’.Рђ. «Разноуровневые задачи», в„– 2/2000.
Основные формулы раздела «Теория относительности»
Относительность промежутков времени
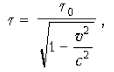
t0 – интервал времени в системе K0;
t – интервал времени относительно системы K.
Относительность расстояний
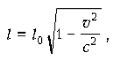
l0 – длина стержня в системе K0;
l – длина стержня в системе K.
Сложение скоростей в СТО
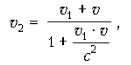
v1 – скорость тела относительно системы K1;
v2 – скорость тела относительно системы K;
v – скорость системы K1 относительно системы K.
Связь между энергией, импульсом и массой
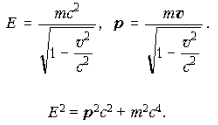
Рнергия РїРѕРєРѕСЏ тела
E0 = m c2.