КОНТРОЛЬ
Р—РќРђРќРР™
|
Задачи из-за
РєРѕСЂРґРѕРЅР°
Закон сохранения
импульса. Системы из нескольких тел.
Столкновения
Задача о катушке
 Проанализируйте
движение катушки ниток, когда вы тянете за нитку: а) вертикально
вверх, б) горизонтально. Как влияет на
движение величина силы, с которой вы тянете
нитку?
Проанализируйте
движение катушки ниток, когда вы тянете за нитку: а) вертикально
вверх, б) горизонтально. Как влияет на
движение величина силы, с которой вы тянете
нитку?
Analyze the motion of the spool in Figure as you pull
the thread: (a) directly upward; (b) horizontally. Consider the effect on the motion of
how hard you pull.
 Ответ 1. Базовый уровень
Ответ 1. Базовый уровень
Вращение происходит вокруг
мгновенной оси, проходящей через т. О. Угловая
скорость относительно этой мгновенной оси
вращения есть 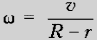 ,
где v – скорость поступательного движения
катушки, R – радиус катушки, r – радиус
«намотки». Отсюда
,
где v – скорость поступательного движения
катушки, R – радиус катушки, r – радиус
«намотки». Отсюда 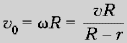 . Катушка будет двигаться относительно
точки O в ту сторону, в которую направлена
сила натяжения нити. Если нить находится наверху
(Т2), то
. Катушка будет двигаться относительно
точки O в ту сторону, в которую направлена
сила натяжения нити. Если нить находится наверху
(Т2), то 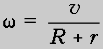 , т.е. скорость ее перемещения будет
меньше, чем когда нить внизу (Т1).
Если тянуть вверх слева (Т3), то
катушка покатится вправо. Если тянуть вверх
справа (Т4), то катушка покатится
влево.
, т.е. скорость ее перемещения будет
меньше, чем когда нить внизу (Т1).
Если тянуть вверх слева (Т3), то
катушка покатится вправо. Если тянуть вверх
справа (Т4), то катушка покатится
влево.
Л.Н.Кондратьев, канд.
физ.-мат. наук
Ответ 2. Углубленный уровень
К сожалению, дать краткий, не
вызывающий сомнений и дальнейших вопросов, ответ
на поставленные в задаче как будто простые
вопросы едва ли возможно, как и в большинстве
задач о движении протяженных тел, где
перемещение сопровождается вращением и где
существенную роль играют силы трения. Достаточно
убедительный ответ требует предварительного
обсуждения и количественного рассмотрения.
Прежде чем начинать
теоретически объяснять поведение катушки в
предлагаемых ситуациях, рекомендуем читателю
самому проделать опыты с настоящей катушкой и
убедиться, насколько «хитро» она ведет себя в
зависимости от положения свободного конца нитки
относительно катушки, от угла его наклона
относительно поверхности стола и от силы
натяжения нити. Соответствующая теоретическая
задача так и называется: задача о «хитрой»
катушке. Здесь предложены только два ее частных
случая, причем требующие уточнения.
Прежде всего договоримся
считать катушку твердым (недеформируемым) телом.
Первое предварительное замечание касается
описания движения твердого тела. Нас будут в
особенности интересовать однородные
осесимметричные, для краткости – «круглые», тела
типа катушек, колес, цилиндров и т.п., у которых
центр масс (ц.м.) лежит на оси симметрии. Движение
твердого тела сводится к движению его ц.м.
(перемещению) под действием внешних сил и к
вращению относительно ц.м. под действием
моментов этих сил. Сравнительно просто
описывается так называемое плоское движение,
когда каждая частица твердого тела движется в
фиксированной, своей для каждой частицы,
плоскости. Частным случаем плоского движения
является движение круглых тел перпендикулярно
оси симметрии, при этом ось симметрии остается
параллельной самой себе, а ц.м. остается в одной
плоскости. В этом случае уравнения движения
сводятся к двумерным, плоским, уравнениям
Ньютона для ц.м. и к уравнению моментов
относительно РѕСЃРё симметрии. Рменно этот случай
будет интересовать нас более всего.
Второе общее замечание
касается поведения круглых тел на поверхностях.
Для определенности будем говорить о катушке на
горизонтальной поверхности стола, с которой
катушка соприкасается, или контактирует, нижними
точками двух своих торцевых ободьев. Ниже для
краткости мы будем называть их точками контакта.
Аналогичное рассмотрение справедливо для любого
круглого тела на любой поверхности при их
точечном (колесо) или линейном (цилиндр) контакте.
В общем случае движение
катушки по поверхности стола носит достаточно
сложный характер. В зависимости от действующих
на нее внешних сил и от начальных условий
(начальных положений ц.м. и начальных скоростей
перемещения и вращения) катушка может катиться
по поверхности стола, вращаясь вокруг своей оси,
может скользить по этой поверхности,
поворачиваться вокруг вертикальной оси, причем
все три вида движения могут совмещаться; наконец,
катушка может подпрыгивать над столом. Напомним,
что собственно качением (чистым качением)
называется такое плоское движение, когда катушка
движется, вращаясь вокруг своей оси, при этом
точки контакта имеют нулевую скорость
относительно стола*.
При качении величина скорости
перемещения катушки v = Rw, где R – радиус
РѕР±РѕРґР°, w
– величина угловой скорости вращения. При
скольжении скорость точек контакта относительно
стола отлична от нуля. При чистом скольжении
катушка не вращается вокруг оси. Если же она еще и
вращается, говорят о качении с проскальзыванием,
или просто проскальзывании. Мы будем употреблять
именно этот термин. При проскальзывании может
быть как v > wR, так и v < wR (в
последнем случае, если речь идет, например, о
колесах автомобиля, говорят, что автомобиль
«буксует»).
Третье общее замечание
относится к внешним силам, действующим на
круглое тело, находящееся на поверхности, в
особенности к силам трения. В рассматриваемом
нами случае действующие на катушку силы – это
сила тяжести, сила натяжения нити и сила
взаимодействия со столом. Сила взаимодействия
катушки с поверхностью стола приложена в точках
контакта и содержит вертикальную составляющую
(привычную «реакцию опоры») и горизонтальную
составляющую, которую традиционно называют
силой трения. Сила трения имеет сложную (и до
конца еще не выясненную) природу, причем сила
трения, определяя движение, сама зависит от
характера движения – качения или
проскальзывания.
Различают три вида силы
трения: сила трения сцепления, сила трения
качения и сила трения скольжения.
Сила трения сцепления
проявляется при качении, она аналогична силе
трения сцепления РїСЂРё контакте плоских тел. Рта
сила возникает как реакция на внешнее
воздействие, именно, направление этой силы в
каждой точке контакта тела (катушки) с
поверхностью противоположно тангенциальному
(касательному к поверхности) ускорению этой
точки контакта, которое она имела бы под
воздействием только внешних сил без трения: из-за
сцепления с поверхностью тело в точках контакта
воздействует на нее в направлении ускорения,
соответственно, по 3-му закону Ньютона, возникает
противоположная сила со стороны поверхности на
катящееся тело – это и есть сила трения
сцепления. Можно сказать, что тело
«отталкивается» от поверхности, в результате
скорость точек контакта при качении остается
равной нулю. Сила трения сцепления может
ускорять и замедлять перемещение тела (катушки),
т.е. движение его ц.м., эта сила не совершает
работы и с ней не связаны потери энергии (переход
энергии движения в тепло). Величина Fсц
этой силы трения определяется прочими внешними
силами из условия отсутствия проскальзывания,
она может принимать любое значение в интервале
от нуля до некоторого максимального значения:
0 Р€ FСЃС† Р€ FСЃС†.
макс = mN, где N – величина силы
нормального давления на поверхность стола в
точке контакта, m – коэффициент трения.
При больших внешних
воздействиях сила трения сцепления не может
обеспечить чистое качение, и имеет место
проскальзывание. При проскальзывании действует
сила трения скольжения, она всегда препятствует
проскальзыванию, но может как замедлять
перемещение тела, так и ускорять его: в качестве
известного всем примера последнего является
движение по земле предварительно раскрученного
обруча, тот же эффект даст на столе
предварительно раскрученная катушка. В первом
приближении величина силы трения скольжения Fск = Fсц.
макс = mN, в действительности она
обычно падает с увеличением скорости
проскальзывания. При проскальзывании
кинетическая энергия движения переходит в тепло.
При качении, а также при
проскальзывании, действует сила трения качения.
Сила трения качения всегда замедляет вращение,
именно она останавливает свободно катящиеся по
горизонтальной поверхности тела. Рта сила
связана с неупругими деформациями в месте
контакта, который уже нельзя считать точечным.
Последнее проявляется в том, что при качении
катушки сила реакции опоры проходит не через ее
ц.м. и создает ненулевой момент относительно оси
вращения, тормозящий вращение. С трением качения
также связаны потери энергии на тепло. Трение
качения уменьшается с гладкостью и твердостью
соприкасающихся тел. Для гладких и твердых тел
сила трения качения обычно много меньше по
величине прочих сил трения.
Наконец, последнее, четвертое,
замечание: о взаимном влиянии характера движения
и сил трения; этот момент хотелось бы подчеркнуть
особо. Мы знаем, что движение тела определяется
уравнениями движения (Ньютона), т.е. внешними
силами, и начальными условиями: начальными
положениями и скоростями. При наличии сил трения
дело осложняется тем, что, с одной стороны, силы
трения определяют характер движения, а с другой,
сами силы трения зависят от характера движения,
т.е. зависят в конце концов от прочих внешних сил
и начальных условий. Другими словами, специфика
сил трения состоит в том, что сам вид уравнений
движения зависит не только от прочих внешних сил,
но и от начальных условий: при некоторых
начальных условиях и прочих внешних силах силы
трения одни (например силы трения сцепления), а
при других – другие (например силы трения
скольжения). Причем эта зависимость может быть
критической, носить пороговый характер. Наконец,
силы трения могут изменяться в процессе
движения.
РР· всего сказанного вытекают
следующие общие замечания. Если движение катушки
плоское и начальное положение – положение покоя,
– то при сравнительно небольшой внешней силе
(приложенной не в точках контакта), она катится по
столу, вращаясь, при превышении же некоторого
критического значения внешней силы начинается
проскальзывание. В любом случае движению
препятствует сила трения качения. Если внешняя
сила содержит вертикальную составляющую, то
катушка вообще может оторваться от стола.
Теперь разберем более
подробно движение катушки в предлагаемых
случаях а и б, пренебрегая в первом
приближении трением качения. Движение катушки
предполагается плоским, для этого нужно, чтобы
нитка была намотана посередине катушки (или
поставлена на рельсы). весом нитки пренебрегаем
– сматывание нитки не приводит к изменению массы
и момента инерции катушки. Вначале катушка
покоится.
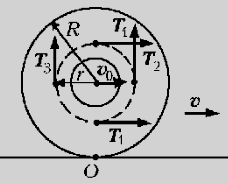
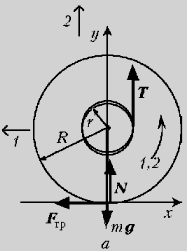 Качественный ответ
представлен на рис. а и б, где показаны
действующие на катушку силы: сила тяжести mg,
реакция опоры N, сила натяжения нити Т
и сила трения Fтр. Светлыми
стрелками изображены направления перемещения
катушки и ее вращения вокруг оси при
сравнительно слабых (индекс 1) и сильных (индекс 2)
натяжениях Т нити.
Качественный ответ
представлен на рис. а и б, где показаны
действующие на катушку силы: сила тяжести mg,
реакция опоры N, сила натяжения нити Т
и сила трения Fтр. Светлыми
стрелками изображены направления перемещения
катушки и ее вращения вокруг оси при
сравнительно слабых (индекс 1) и сильных (индекс 2)
натяжениях Т нити.
Случай а: нитку тянут вверх с
силой T (рис. а). Сила натяжения нити, с
одной стороны, уменьшает реакцию опоры, N = mg
– T, а, с другой – создает вращательный момент
относительно оси катушки, приводящий к
ускоренному вращению катушки против часовой
стрелки. При сравнительно слабом натяжении,
заведомо меньшем веса катушки, T < mg,
катушка остается на столе и точка контакта
должна была бы проскальзывать слева направо, но
этому препятствует сила Fтр = Fсцтрения
сцепления, направленная справа налево и
соответственно ускоряющая катушку в этом
направлении, одновременно замедляя вращение.
Величина Fсц силы трения определяется из
условия отсутствия проскальзывния, она
пропорциональна Т. Катушка ускоренно катится
налево, вращаясь против часовой стрелки, а
ускорение пропорционально натяжению нити Т.
При возрастании T, с одной стороны,
уменьшается N, с другой стороны, растет Fсц,
следовательно, растет ускорение катушки – как
линейное, так и угловое. Но Fсц не может
превышать Fсц. макс = mN. Поэтому при
некотором критическом значении T = Tкр < mg
сила трения сцепления достигает своего
максимального значения Fсц. макс, и при Tкр < T < mg
начинается проскальзывание, сила трения
становится силой трения скольжения, Fтр = Fск,
РІ первом приближении можно считать FСЃРє = mN. Рта сила
падает с ростом T, т.к. N уменьшается,
соответственно уменьшается ускорение
горизонтального перемещения катушки, обращаясь
в нуль при T = mg. Наконец, при T > mg
катушка будет ускоренно двигаться вверх,
одновременно ускоренно раскручиваясь вокруг
РѕСЃРё.
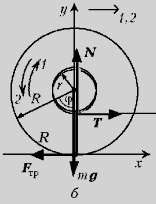 Случай б: нитку тянут
горизонтально (рис. б). В этом случае
нормальное давление N = mg и постоянно.
Сила натяжения нити ускоряет катушку направо и
одновременно сообщает ей ускоренное вращение
вокруг оси против часовой стрелки. Опять-таки
точка контакта должна была бы проскальзывать
слева направо. Ртому препятству-ет сила трения
сцепления, действующая справа налево,
замедляющая ускорение перемещения и создающая больший
момент вращения по часовой стрелке. В
результате при сравнительно малых T катушка
ускоренно катится без проскальзывания слева
направо. С ростом T величина Fсц силы
трения нарастает, пока при некотором критическом
значении T = Tкр1 не достигнет
своего максимального значения Fсц. макс = mmg. При T > Tкр1
начинается проскальзывание, сила трения
становится практически постоянной силой трения
скольжения, Fтр = Fск = mmg, не
зависящей от T. Катушка скользит направо,
одновременно вращаясь по часовой стрелке. Но с
дальнейшим ростом T это вращение замедляется,
т.к. нарастает вращающий против часовой стрелки
момент силы натяжения нити, пока наконец после
некоторого второго критического значения T > Tкр2
вращение не переходит во вращение против часовой
стрелки.
Случай б: нитку тянут
горизонтально (рис. б). В этом случае
нормальное давление N = mg и постоянно.
Сила натяжения нити ускоряет катушку направо и
одновременно сообщает ей ускоренное вращение
вокруг оси против часовой стрелки. Опять-таки
точка контакта должна была бы проскальзывать
слева направо. Ртому препятству-ет сила трения
сцепления, действующая справа налево,
замедляющая ускорение перемещения и создающая больший
момент вращения по часовой стрелке. В
результате при сравнительно малых T катушка
ускоренно катится без проскальзывания слева
направо. С ростом T величина Fсц силы
трения нарастает, пока при некотором критическом
значении T = Tкр1 не достигнет
своего максимального значения Fсц. макс = mmg. При T > Tкр1
начинается проскальзывание, сила трения
становится практически постоянной силой трения
скольжения, Fтр = Fск = mmg, не
зависящей от T. Катушка скользит направо,
одновременно вращаясь по часовой стрелке. Но с
дальнейшим ростом T это вращение замедляется,
т.к. нарастает вращающий против часовой стрелки
момент силы натяжения нити, пока наконец после
некоторого второго критического значения T > Tкр2
вращение не переходит во вращение против часовой
стрелки.
В обоих рассматриваемых
случаях сила трения качения уменьшает как
линейное ускорение поступательного движения,
так и угловое ускорение вращения.
Возможно, приведенный
качественный ответ не удовлетворит
любознательного читателя, особенно в части,
касающейся промежуточных величин силы
натяжения. Для интересующихся приведем
количественное аналитическое решение обеих
задач в пренебрежении силой трения качения, не
только потому, что эта сила при твердой катушке и
твердом покрытии стола обычно много меньше
прочих сил трения, но и потому еще, что для нее не
существует достаточно общих аналитических
формул. Пусть m – масса катушки, I – момент
инерции катушки относительно ее оси, R –
радиус обода катушки, r – радиус бобины (r < R),
j – угол
поворота вокруг оси, отсчитываемый по часовой
стрелке.
Случай а. Уравнения
движения включают два уравнения движения
Ньютона для ц.м., по осям x и y
соответственно:
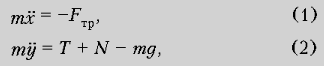
и уравнение моментов для
вращения вокруг оси:
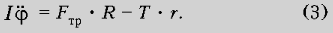
При сравнительно малых T,
заведомо при T < mg, имеем согласно (2)
у = 0 (катушка находится на столе) и
соответственно N = mg – T. Сила
трения есть сила трения сцепления Fтр = Fсц Ј mN, и имеет
место качение (без проскальзывания), при котором
линейная скорость центра масс и угловая скорость
связаны соотношением 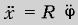 , откуда следует связь
ускорений, линейного и углового:
, откуда следует связь
ускорений, линейного и углового:

Подставляя в (3)
последовательно (4) и (1), получаем:
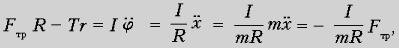
откуда:
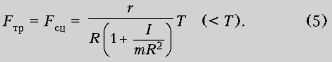
Соответственно:
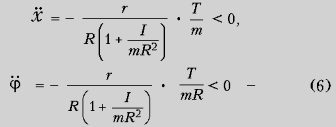
катушка с постоянным
ускорением, линейным и угловым, катится налево.
Выписанные соотношения (5) справедливы, пока Fтр = Fсц Ј mN = m(mg – T),
С‚.Рµ. РїСЂРё:
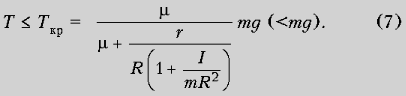
РџСЂРё TРєСЂ < T < mg
величина силы трения Fтр = Fсц.
макс = mN, и из (1) и (3) получаем:
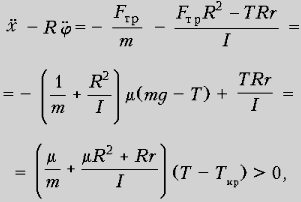
стало быть, и 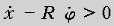 – имеет место
проскальзывание, катушка крутится против
часовой стрелки быстрее, чем смещается налево,
сила трения есть сила трения скольжения.
– имеет место
проскальзывание, катушка крутится против
часовой стрелки быстрее, чем смещается налево,
сила трения есть сила трения скольжения.
При этом сами ускорения имеют
РІРёРґ:
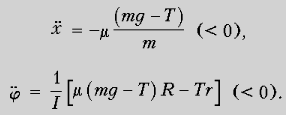
РџСЂРё T С– mg
нормальное давление N обращается в нуль, а с
ним и сила трения, Fтр = 0. Поэтому
согласно уравнениям движения (1)–(3) получаем:
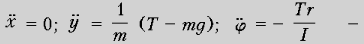
катушка ускоренно
поднимается вверх, одновременно ускоренно
раскручиваясь (разматываясь) против часовой
стрелки.
Случай б. Нормальное
давление компенсирует вес тела, перемещение
катушки одномерно – вдоль оси x. Уравнения
движения имеют вид:
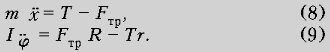
Опять-таки, пока T мало,
имеет место качение, когда 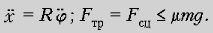 В этом случае из
(8), (9) следует:
В этом случае из
(8), (9) следует:
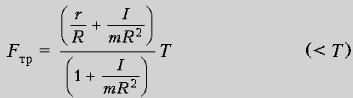
и соответственно:
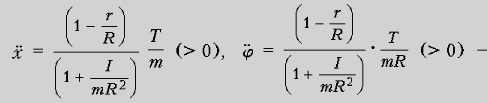
катушка с постоянным линейным
и угловым ускорениями катится направо
(любопытно, что если катушку поставить на рельсы
и сделать радиус намотки больше радиуса ободьев, r
> R, то катушка покатится налево!).
Ртот режим имеет место, РїРѕРєР° Fтр Р€ mmg, С‚.Рµ. РїРѕРєР°
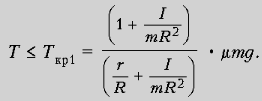
Заметим, что 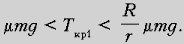 При T > Tкр1
имеет место проскальзывание: Fтр = Fск = mmg;
РџСЂРё T > TРєСЂ1
имеет место проскальзывание: Fтр = Fск = mmg; 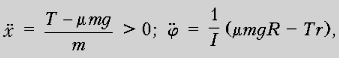 при
этом:
РїСЂРё
этом:
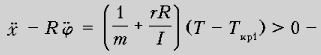
катушка смещается быстрее,
чем крутится. Более того, при 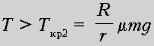 катушка крутится уже против
часовой стрелки!
катушка крутится уже против
часовой стрелки!
Вот такая «хитрая» катушка...
Б.Л. Воронов, доктор физ.-мат.
наук

 Проанализируйте
движение катушки ниток, когда вы тянете за нитку: а) вертикально
вверх, б) горизонтально. Как влияет на
движение величина силы, с которой вы тянете
нитку?
Проанализируйте
движение катушки ниток, когда вы тянете за нитку: а) вертикально
вверх, б) горизонтально. Как влияет на
движение величина силы, с которой вы тянете
нитку? Ответ 1. Базовый уровень
Ответ 1. Базовый уровень Качественный ответ
представлен на рис. а и б, где показаны
действующие на катушку силы: сила тяжести mg,
реакция опоры N, сила натяжения нити Т
и сила трения Fтр. Светлыми
стрелками изображены направления перемещения
катушки и ее вращения вокруг оси при
сравнительно слабых (индекс 1) и сильных (индекс 2)
натяжениях Т нити.
Качественный ответ
представлен на рис. а и б, где показаны
действующие на катушку силы: сила тяжести mg,
реакция опоры N, сила натяжения нити Т
и сила трения Fтр. Светлыми
стрелками изображены направления перемещения
катушки и ее вращения вокруг оси при
сравнительно слабых (индекс 1) и сильных (индекс 2)
натяжениях Т нити. Случай б: нитку тянут
горизонтально (рис. б). В этом случае
нормальное давление N = mg и постоянно.
Сила натяжения нити ускоряет катушку направо и
одновременно сообщает ей ускоренное вращение
вокруг оси против часовой стрелки. Опять-таки
точка контакта должна была бы проскальзывать
слева направо. Ртому препятству-ет сила трения
сцепления, действующая справа налево,
замедляющая ускорение перемещения и создающая больший
момент вращения по часовой стрелке. В
результате при сравнительно малых T катушка
ускоренно катится без проскальзывания слева
направо. С ростом T величина Fсц силы
трения нарастает, пока при некотором критическом
значении T = Tкр1 не достигнет
своего максимального значения Fсц. макс = mmg. При T > Tкр1
начинается проскальзывание, сила трения
становится практически постоянной силой трения
скольжения, Fтр = Fск = mmg, не
зависящей от T. Катушка скользит направо,
одновременно вращаясь по часовой стрелке. Но с
дальнейшим ростом T это вращение замедляется,
т.к. нарастает вращающий против часовой стрелки
момент силы натяжения нити, пока наконец после
некоторого второго критического значения T > Tкр2
вращение не переходит во вращение против часовой
стрелки.
Случай б: нитку тянут
горизонтально (рис. б). В этом случае
нормальное давление N = mg и постоянно.
Сила натяжения нити ускоряет катушку направо и
одновременно сообщает ей ускоренное вращение
вокруг оси против часовой стрелки. Опять-таки
точка контакта должна была бы проскальзывать
слева направо. Ртому препятству-ет сила трения
сцепления, действующая справа налево,
замедляющая ускорение перемещения и создающая больший
момент вращения по часовой стрелке. В
результате при сравнительно малых T катушка
ускоренно катится без проскальзывания слева
направо. С ростом T величина Fсц силы
трения нарастает, пока при некотором критическом
значении T = Tкр1 не достигнет
своего максимального значения Fсц. макс = mmg. При T > Tкр1
начинается проскальзывание, сила трения
становится практически постоянной силой трения
скольжения, Fтр = Fск = mmg, не
зависящей от T. Катушка скользит направо,
одновременно вращаясь по часовой стрелке. Но с
дальнейшим ростом T это вращение замедляется,
т.к. нарастает вращающий против часовой стрелки
момент силы натяжения нити, пока наконец после
некоторого второго критического значения T > Tкр2
вращение не переходит во вращение против часовой
стрелки.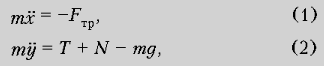
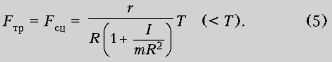
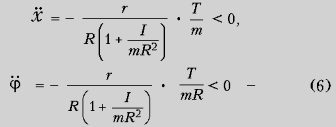
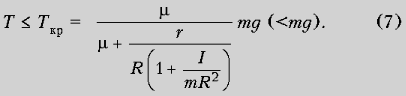
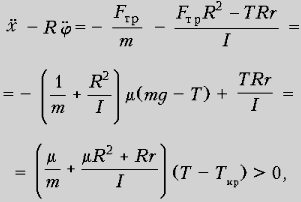
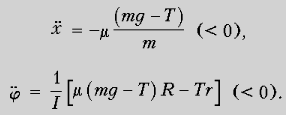
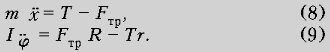
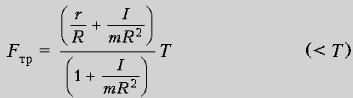
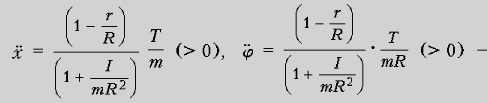
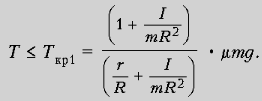
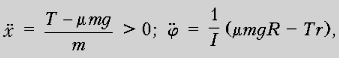 РїСЂРё
этом:
РїСЂРё
этом: