Задача для учителя

Р’ серии статей РїРѕРґ общим названием «В университет!В» «Физика» публикует задачи, предлагавшиеся РІ разные РіРѕРґС‹ РЅР° вступительных экзаменах РІ МГУ. Внимание привлекла интересная задача РїРѕ оптике, авторское решение которой занимает почти половину газетной страницы (РЁРёСЂРѕРєРѕРІ Рђ.Рђ. Рё РґСЂ.,в„– 2/2000). Громоздкость этого РјРЅРѕРіРѕС…РѕРґРѕРІРѕРіРѕ анализа, РІСЂСЏРґ ли целесообразного именно РЅР° вступительном экзамене, вызывает РІРѕРїСЂРѕСЃ – какова доля абитуриентов, успешно справившихся СЃ этой головоломкой? Ведь предложенный СЃРїРѕСЃРѕР± решения РЅРµ самый рациональный. Именно поэтому такая задача может быть полезна учителю физики, особенно РІ классах углубленного изучения предмета. Умение пойти СЃРІРѕРёРј путем, увидеть разные варианты представляется РѕРґРЅРёРј РёР· наиболее ценных качеств учащегося, это умение можно Рё нужно воспитывать, поощряя каждую попытку действовать самостоятельно.

Р’РѕС‚ условие задачи: «Перемещая линзу между экраном Рё предметом, удается получить РґРІР° его четких изображения поперечными размерами 2 СЃРј Рё 8 СЃРј. Найдите поперечный размер предмета». РќРµ самая удачная формулировка. РќРµ «удается», Р° всегда возможно, лишь Р±С‹ расстояние РѕС‚ предмета РґРѕ экрана было РЅРµ меньше четырех фокусных расстояний данной линзы. Еще хуже СЂРёСЃСѓРЅРѕРє, нижняя половина которого получена, РІРёРґРёРјРѕ, переворотом верхней РЅР° компьютере, РІ результате чего предмет приобрел различную высоту («поперечный размер»), РґР° Рё горизонтальное смещение половинок РґСЂСѓРі относительно РґСЂСѓРіР° тоже РЅРµ обязательно. РџСЂРёРІРѕРґРёРј правильный СЂРёСЃСѓРЅРѕРє.

Поскольку линза одна и та же, приравняем фокусные расстояния, выраженные для первого и второго положений:

где S – величина перемещения линзы. И здесь мы покидаем авторов.

Упростим выражение (1):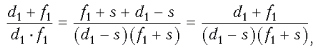

d₁f₁ = (d₁ вЂ“ s)(f₁ + s) =  d₁f₁ + d₁s вЂ“ f₁s вЂ“ s₂,

s = d₁ вЂ“ f₁.

Из СЂРёСЃСѓРЅРєР° РІРёРґРЅРѕ, что d₂ = d₁ вЂ“ s, Р°  f₂ = f₁ + s, откуда: d₂ = d₁ вЂ“ d₁ + f₁ = f₁; f₂ =  f₁ + d₁ вЂ“ f₁ = d₁ Р® d₂ = f₁; f₂ = d₁.

А из подобия соответствующих треугольников увеличение линзы в двух положениях есть .

Их произведение равно, естественно, единице:

Вот и все решение.

Однако учителю полезно проделать еще некоторые преобразования и получить так называемую формулу Бесселя, пригодную для исследования не только тонких, но и реальных линз. Перепишем исходную формулу:

Рё преобразуем ее: 

Эта формула хороша тем, что расстояние от предмета до экрана измеряется независимо от положения линзы, и перемещение линзы одно и то же для всех точек, жестко связанных с линзой, т.е. не нужно знать положение оптического центра линзы, от которого следует отсчитывать расстояния... Именно поэтому способ Бесселя применим для любой линзы, не только для тонкой.