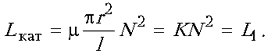
РњС‹ неоднократно подчеркивали важность понимания таких параметров, как коэффициент самоиндукции (индуктивность) Рё взаимная индуктивность. Р’ моей статье «Магнитный терменвокс» (в„– 21/2000) предлагались опыты, позволяющие наглядно продемонстрировать учащимся, что величина индуктивности определяется магнитными свойствами окружающего пространства Рё геометрической формой контура СЃ током РІ этом пространстве. Принятое определение индуктивности L как величины, характеризующей РДС самоиндукции, которая возникает РІ контуре РїСЂРё изменении силы тока, дополняется выражением для магнитной энергии, накопленной РІ катушке индуктивности.
В теоретической физике коэффициент самоиндукции (индуктивность) вводится при вычислении (рассмотрении) энергии системы токов, поэтому ряд задач в электродинамике проще решать с учетом преобразования одного вида энергии в другой. Рассмотрим происходящие физические явления в задаче «электромагнитная пушка».
При подключении катушки с сердечником к сети 220 В в катушке накапливается магнитная энергия, пропорциональная индуктивности и квадрату тока. Устанавливая проводящее кольцо на сердечник, мы изменяем индуктивность катушки. Так как магнитный поток в этом «витке» катушки противоположен общему магнитному потоку в сердечнике, то это приводит к уменьшению индуктивности.
Рндуктивность катушки без кольца (обозначения, как Сѓ РЎ.Варламова):
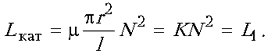
Оценка индуктивности L2 (при надетом кольце) задача достаточно сложная, но общий подход к вычислению таков. Катушка трансформатора и кольцо имеют общий магнитный поток, характеризуемый коэффициентом взаимной индуктивности
Рндуктивность кольца РЅР° сердечнике L~KN2 РїСЂРё N = 1, РЅРѕ это РІРѕРІСЃРµ РЅРµ соответствует действительно РѕРґРЅРѕРјСѓ витку. Введем подгоночный параметр a2, который подбирается экспериментально, Рё обозначим индуктивность кольца как L=a2K. Отсюда:
– коэффициент взаимной индуктивности
– индуктивность катушки с надетым кольцом
Зная индуктивности L2 Рё L1, можно вычислить изменение магнитной энергии катушки РїСЂРё подскакивании кольца. Рто изменение магнитной энергии равно кинетической энергии кольца, которая переходит РІ потенциальную энергию кольца РІ гравитационном поле Земли. Таким образом, DW = mgh, РіРґРµ mg – вес кольца, h – высота его подскакивания.
Ток катушки в основном определяется ее
индуктивностью: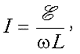 
так что
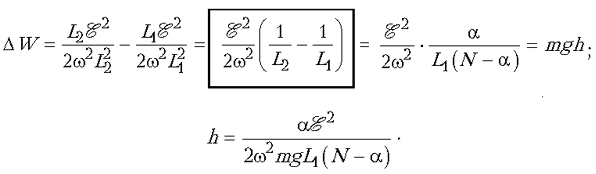
Приведем грубую оценку высоты подскакивания кольца при
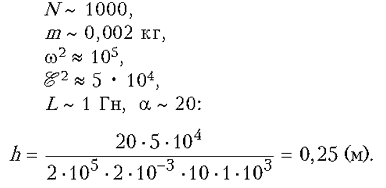
Точнее и проще оценить h, измерив предварительно индуктивности L1 и L2 и взвесив кольцо.
Теоретически высота h наибольшая при N=1. Однако реально надо учитывать технические характеристики источника напряжения, свойства материалов (электрическое сопротивление и механическую прочность витков), т.к. магнитное поле витков стремится разорвать кольца.
Трудно согласиться с мнением автора о времени разгона кольца, т.к. основное ускорение кольцо получает на пути около 1–2 см, соответственно за первый период колебания напряжения.
Действительно, если кольцо приобретает
кинетическую энергию 
и взлетает на высоту h, то:
– его максимальную скорость вычислим так:
– время полетаt =
– ускорение при разгоне получим из равенствагде l – путь разгона:
– время разгона
.
