Интересные задачи

Турнир юных физиков (ТЮФ)

 

 


Команда СУНЦ УрГУ – победительница XXIV Всероссийского турнира юных физиков.
Слева направо: Инишева Ольга Викторовна – преподаватель, Колмогорова Аня, Ивлев Артем, Ахматханов Андрей, Булатов Коля, Куприн Саша. Все дети – ученики 10-го класса «В» СУНЦ УрГУ

Краткая история

РўСѓСЂРЅРёСЂ юных физиков (ТЮФ) – командное соревнование учащихся старших классов РІ решении физических проблем. Р’ Р РѕСЃСЃРёРё РѕРЅ ежегодно проводится уже РІ течение 24 лет, РёР· РЅРёС… 15 лет – СЃ участием зарубежных команд. Международные соревнования курируются ЮНЕСКО. Первый ТЮФ состоялся РІ марте 1979 Рі. как логическое продолжение физбоев между сборными командами РњРѕСЃРєРІС‹ Рё Черноголовки, РІ нем приняли участие 7 РєРѕРјР°РЅРґ РёР· РњРѕСЃРєРІС‹ Рё РџРѕРґРјРѕСЃРєРѕРІСЊСЏ. Р’ начале 80-С… РіРі. РІ турнире стали принимать участие команды РёР· РґСЂСѓРіРёС… РіРѕСЂРѕРґРѕРІ РЎРЎРЎР , РѕРЅ получил статус Всесоюзного. РќР° Всесоюзные ТЮФы собиралось РґРѕ 30 команд. Организаторы турнира стали лауреатами премии Ленинского комсомола. Р’ 1987 Рі. РЅР° ТЮФ прибыли команды РёР· РґСЂСѓРіРёС… государств, Рё РѕРЅ стал международным.

Задания турнира формируются международным оргкомитетом (председатель Г.Тибелл, Швеция). В состав этого оргкомитета входят председатели национальных оргкомитетов. Председателем Российского оргкомитета ТЮФа является В.И.Лобышев (Москва, МГУ). Заседания международного оргкомитета проводятся в начале октября каждого года в стране, принимающей турнир будущего года. Турнир 2003 г. будет проходить в Швеции, поэтому семинар по подготовке задач состоялся в начале октября именно там. Как правило, задания турнира включают 17 задач, которые отбираются из числа задач, присланных национальными оргкомитетами. Так, например, при формировании задания ТЮФа 1999 г. было рассмотрено более 180 задач.

Российский турнир проводится по заданиям международного, как правило, на базе одного из четырех специализированных учебно-научных центров при крупных университетах – Московском, Санкт-Петербургском, Уральском (Екатеринбург) и Новосибирском. Международный ТЮФ проводится в конце мая–начале июня, Российский турнир – в марте. В некоторых городах и областях в январе проводятся локальные турниры.

В последние годы на Всероссийских турнирах наиболее широко представлены команды из Свердловской области. Это неудивительно, ведь в последние шесть лет на территории этой области совместными усилиями Минобразования и СУНЦ УрГУ ежегодно проводится открытый областной турнир. Команды школы-лицея № 130 и гимназии № 9 г. Екатеринбурга неоднократно завоевывали призовые места, а команда СУНЦ УрГУ является шестикратной победительницей Всероссийского турнира и неоднократно представляла Россию на международном турнире. В 2000 г. (Будапешт) она заняла 2-е место, в 2001 г. (Хельсинки) – 3-е. Перед этим последнее успешное выступление российских команд произошло в 1994 г. в Голландии (1-е место, СУНЦ МГУ, Москва).

Особенности турниров

Форма проведения, характер предлагаемых задач, требования к участникам существенно отличают ТЮФ от обычных физических олимпиад. Большинство задач турнира не имеют известных и однозначных решений. Длительный срок их подготовки (несколько месяцев вместо нескольких часов) позволяет учащимся провести необходимые физические опыты, ознакомиться с литературой, разработать свой подход к проблеме. При этом дети работают в режиме, наиболее приближенном к научным исследованиям. Поскольку заранее известного ответа на вопросы, поставленные в задачах, не существует, то участникам приходится выдвигать свои оригинальные гипотезы, объясняющие физическое явление, проверять их в ходе экспериментов, проводить измерения физических величин. Им приходится оценивать погрешности, оптимизировать созданные ими же экспериментальные установки, выбирать наиболее точный и рациональный метод измерения. Для решения некоторых задач вполне достаточно домашней лаборатории, для решения других требуется создание специальных экспериментальных установок, которые хотя и не очень сложны, но требуют работы «руками».

При решении многих задач участники турнира используют компьютер. Очень часто вычислительная техника применяется не только для облегчения громоздких расчетов, но и для моделирования физических процессов. В рамках традиционных олимпиад осуществить подобное практически невозможно. Многие задачи предполагают знание не только физики, но и смежных с ней дисциплин – астрономии, биологии, химии.

Во время турнира участникам предстоит выступить с докладом, защищая собственное решение задачи, поспорить с оппонентами и рецензентами, оценить положительные и отрицательные моменты в решениях этих же задач другими командами. При подготовке доклада учащиеся получают навыки работы в некоторых программных пакетах, т.к. им необходимо изготавливать плакаты, слайды, тексты докладов.

Участники команд получают также навык по работе с видео- и фотооборудованием, которое используется для наглядного представления экспериментов и опытов. Кроме того, использование видеозаписи оказывается необходимым для исследования быстро протекающих процессов, что позволяет школьникам провести необходимые измерения.

Регламент турнира

Состав команды – 5 учащихся (школ, лицеев, техникумов, училищ и других средних образовательных учреждений). Команда возглавляется капитаном.

ТЮФ проводится в форме физбоев. Как правило, проводятся 3–5 отборочных боев и финальный бой. Количество физбоев зависит от числа команд, принимающих участие в турнире.

Оптимальное число команд для одного физбоя – 3. В ходе любого физбоя в различных его действиях команда выступает в роли докладчика, оппонента и рецензента.

РҐРѕРґ физбоя примерно следующий. Сначала проводится жеребьевка команд Рё распределение РїРѕ ее итогам ролей РЅР° первое действие. Р’ начале первого действия команда в„– 2 (оппонент) предлагает команде в„– 1 (докладчику) рассказать решение какой-либо задачи. Члены команды в„– 1 совещаются Рё либо отказываются РѕС‚ задачи, либо принимают вызов. Если РїСЂРѕРёСЃС…РѕРґРёС‚ отказ, то процедура вызова повторяется СЃРЅРѕРІР°. Если же команда в„– 1 принимает вызов, то кто-РЅРёР±СѓРґСЊ РёР· членов команды делает доклад РїРѕ предложенной задаче. После окончания доклада оппонент задает РІРѕРїСЂРѕСЃС‹ докладчику. Между РЅРёРјРё РїСЂРѕРёСЃС…РѕРґРёС‚ РґРёСЃРєСѓСЃСЃРёСЏ, РІ С…РѕРґРµ которой докладчик защищает СЃРІРѕРµ решение, Р° оппонент пытается РІ нем разобраться Рё оценить. Заключительный этап любого действия – выступление рецензента (команда в„– 3), который РІ С…РѕРґРµ своего выступления отмечает положительные Рё отрицательные моменты доклада Рё оппонирования. Затем жюри выставляет оценки. Р’ С…РѕРґРµ второго действия роли меняются: команда в„– 1 становится рецензентом, команда в„– 2 – докладчиком, Р° команда в„– 3 – оппонентом. Р’ третьем действии команда в„– 1 – оппонент, в„– 2 – рецензент, в„– 3 – докладчик.

Таблица отборочных боев составляется таким образом, чтобы команды, встретившись друг с другом в ходе одного физбоя, в других боях уже не встречались.

В финал попадают три команды, победившие по итогам отборочных боев.

В ходе физбоев на турнирах учащиеся выступают с докладами, учатся отстаивать свою точку зрения, грамотно и правильно говорить, представлять свои проекты решения физических проблем. Они также учатся оценивать свои решения, поскольку имеют возможность в ходе живой дискуссии со своими сверстниками сравнивать различные подходы к одним задачам. Они учатся правильно формулировать вопросы и отвечать на них. Ведь форма проведения турнира – устная, а дискуссия и оппонирование ведутся командами без предварительной подготовки, «в прямом эфире».

Достаточно зрелищная и живая форма проведения турнира всегда собирает большое число зрителей и болельщиков из числа учащихся и учителей.

XXIV Всероссийский ТЮФ

Турнир проходил 17–22 марта 2002 г. в г. Сарове Нижегородской области между восемью командами: СУНЦ МГУ (Москва), Академической гимназии СПбГУ (Санкт-Петербург), городов Арзамаса, Пушкина, Новодвинска, Сарова (3 команды) и Свердловской обл. (4 команды: г. Качканара и Заречного, школы-лицея № 130 г. Екатеринбурга и СУНЦ УрГУ).

1-е место заняла команда СУНЦ УрГУ в составе:

Андрей Ахматханов (капитан),
Николай Булатов,
Антон Иевлев,
Анна Колмогорова,
Александр Куприн.

Руководители команды: Григорий Максович Миньков и Ольга Викторовна Инишева.

Две лучшие команды (СУНЦ УрГУ и г. Сарова) получили право представлять Россию на международном турнире.

XV Международный ТЮФ

Турнир проходил 23–30 мая 2002 г. в г. Одессе (Украина). В нем приняли участие 20 команд, которые представляли Австралию, Австрию, Беларусь, Болгарию, Венгрию, Германию, Грузию, Корею, Мексику, Нидерланды, Украину, Польшу, Россию, Словакию, Финляндию, Хорватию, Чехию и Швецию. Наша страна была, к сожалению, представлена только одной командой – СУНЦ УрГУ. Каждая команда приняла участие в пяти отборочных боях. В финал вышли три лучшие – Польши, Беларуси и Германии. Победителями этого турнира заслуженно стали польские школьники.

Всероссийские и международные турниры предоставляют школьникам, увлекающимся физикой, из различных городов и стран хорошую возможность для общения. Учителя, подготовившие команды, в ходе турниров могут обменяться опытом, узнать о работе и достижениях своих коллег.

Проблемы

В последнее время при проведении Всероссийских турниров возникли проблемы, во многом связанные с тем, что турнир был исключен из графика Всероссийских олимпиад и конференций. Таким образом, школьники, победившие в турнире и затратившие огромное количество сил на подготовку к нему, оказываются перед выбором: готовиться к международному турниру, чтобы достойно представить нашу страну, либо готовиться к поступлению в вуз. Учителям, подготовившим команды, как правило, «спасибо» никто не говорит.

Непонятно, почему так происходит. Неужели школьник, самостоятельно сумевший разобраться с достаточно сложной физической проблемой, прочитавший большое количество литературы и умеющий применять знания, полученные на уроках, нашим вузам нужен меньше, чем тот, чьи родители своевременно наняли репетиторов? Неужели наши школьные учителя, сумевшие увести с улицы и при двух часах в неделю сумевшие увлечь физикой настолько, что ребенок все вечера проводит в физической лаборатории, не заслужили элементарной благодарности? Чего мы постоянно стесняемся? Да мы гордиться должны! Это в нашей стране, а не где-нибудь
25 лет назад придумали увлекательное соревнование для старшеклассников. Четверть века этот турнир живет в нашей стране и уже 15 лет – на международном уровне. Многие страны, прислав на международный турнир наблюдателей, затем становятся участниками. Иностранцы почему-то очень дорожат турниром и активно в нем участвуют. А мы можем не прислать на турнир команду просто потому, что нет средств. Наши ребята могут не поехать на турнир, потому что им надо сдавать выпускные экзамены. А когда-то (когда турниры проводились под эгидой комсомола) на Всесоюзные турниры собиралось около 30 команд!

Вниманию Руководителей школ, образовательных учреждений, учителей физики и старшеклассников!

XXV Всероссийский ТЮФ будет проходить в г. Екатеринбурге в СУНЦ УрГУ с 17 по 23 марта 2003 г.
XVI Международный турнир юных физиков будет проводиться в Швеции с 1 по 8 июля. Для участия в турнире необходимо подготовить решения задач, которые можно получить в оргкомитете турнира. Если вас заинтересовала информация о турнирах и вы хотели бы принять участие в турнире 2002/2003 уч.г., обращайтесь в один из локальных оргкомитетов ТЮФа:
Екатеринбург, СУНЦ УрГУ, Инишева Ольга Викторовна, заместитель директора по научной работе.
Тел.: (3432) 410-659; факс: (3432) 412-468; e-mail: inicheva@lyceum.usu.ru; 
Москва, МГУ, проф. Валентин Иванович Лобышев, заведующий кафедрой физики СУНЦ МГУ.
Тел.: (095) 445-5306; e-mail: lob@school.phys.su .
Сайт международного ТЮФа в Интернете: http://www.iypt.org .

ВОПРОСЫ XXV ТУРНИРА ЮНЫХ ФИЗИКОВ

1. Воздушный змей. В ветреный день запустите воздушного змея, удерживаемого одной нитью. Часто можно наблюдать устойчивые траектории змея наподобие восьмерки. Почему воздушный змей движется таким образом? Существуют ли другие стабильные траектории?

2. Дождь. Исследуйте и объясните, как движутся капли дождя по оконному стеклу.

3. Прозрачная пленка. Если печатный текст накрыть прозрачной полиэтиленовой пленкой, то его можно без труда прочесть. При удалении пленки от текста буквы становятся нечеткими, и на некотором расстоянии текст прочесть не удается. Изучите свойства пленки. Какими свойствами пленки объясняется наблюдаемый феномен?

4. Яркие пятна. Выдуйте мыльный пузырь и поместите его на поверхность мыльного раствора. При освещении солнечным светом можно увидеть на поверхности пузыря яркие пятна. Исследуйте феномен и сравните два случая: когда пузырь лежит на поверхности раствора и на поверхности стекла.

5. Граница раздела. Несмешивающиеся жидкости образуют резкую границу раздела фаз. Если поверхностное натяжение двух жидкостей различается, можно наблюдать интересные эффекты. Выдуйте пузыри различного размера в нижней жидкости и проанализируйте их поведение вблизи границы раздела фаз.

6. Замерзание напитков. При открывании охлажденных бутылей с газированной водой она может замерзнуть. Изучите явление и его зависимость от параметров системы.

7. Вибрирующая коробка. Разделите коробку на ряд последовательных ячеек невысокими перегородками. Поместите некоторое количество маленьких металлических шариков в коробку. При вертикальной вибрации коробки шарики будут перескакивать из одной ячейки в другую. В зависимости от частоты и амплитуды колебаний распределение шариков может быть устойчивым и неустойчивым. Исследуйте явление и постройте модель для его обьяснения.

8. «Тепловая машина». Сконструируйте «тепловую машину», содержащую U-образную трубку, частично заполненную водой или другой жидкостью. Одно колено трубки открыто, второе соединяется длинной трубкой с подогреваемой колбой. После выведения из равновесия уровня воды покачиванием U-образной трубки возможно появление устойчивых колебаний уровня воды. От чего зависит частота колебаний? Нарисуйте р,V-диаграмму процесса.

9. Падающая труба. При падении высокой кирпичной трубы она может расколоться на две части до касания поверхности земли. Исследуйте и объясните причины явления.

10. Лампа накаливания. Сопротивление нити лампы накаливания сильно зависит от температуры. Продемонстрируйте сделанный вами прибор, использующий эту характеристику.

11. Рассеяние света. Сконструируйте оптический прибор, способный измерять концентрацию нерастворимых веществ в коллоидных растворах. Используйте его для определения жирности молока.

12. Вареное яйцо. Сконструируйте торсионный вискозиметр и используйте его для выяснения различий вязкоупругих свойств куриных яиц с разным временем варки.

13. Электроосмос. Разработайте устройство для осушения мокрого песка с использованием электрической энергии, но без существенного нагревания.

14. «Летающая тарелка». Найдите и обоснуйте оптимальный способ запуска «летающей тарелки» для достижения максимальной дальности полета.

15. Вихрь. Сделайте коробку, имеющую круглое отверстие и мембрану на противоположной стороне. Заполните ее дымом (например от тлеющего торфа). Ударяя по мембране, создайте вихрь, распространяющийся от отверстия в коробке. Объясните явление и опишите, что произойдет при взаимодействии двух вихрей.

16. Тепло и холод. Существует мнение, что для быстрейшего охлаждения горшочка с пищей лед следует положить сверху, но не снизу. Если это так, оцените преимущество первого метода по сравнению со вторым.

17. Задача Прометея. Опишите и продемонстрируйте прибор, который использовали наши предки для получения огня с помощью трения. Определите время, необходимое для получения огня таким способом.

Решение некоторых задач прошлого турнира

Тепловая машина

Наверное, всем известно, что на тело, полностью погруженное в жидкость, действует выталкивающая сила – сила Архимеда, которая определяется следующим выражением:

Здесь r – плотность жидкости, Vт – объем тела. Характер движения тела в жидкости зависит от соотношения силы тяжести и силы Архимеда. Как мы видим, сила Архимеда прямо пропорциональна объему тела Vт, значит, для тела переменного объема, но постоянной массы можно получить различные соотношения силы Архимеда и силы тяжести, изменяя его объем. В нашем случае таким телом является ампула, закрытая резиновым колпачком. Внутри ампулы находится газ – воздух, смешанный с насыщенными парами спирта, и капля спирта в виде жидкости. При изменении температуры этого газа некоторая часть жидкости испарится (или некоторая часть пара конденсируется), т.е. пар станет насыщенным. Давление внутри ампулы также существенно изменится, а вследствие этого изменится и объем колпачка.

Итак, при наливании воды в сосуд сначала наливается горячая вода, а затем – холодная. Конечно, сразу начнет происходить конвекция, но все же распределение температуры некоторое время будет сохраняться. При опускании ампулы в верхний холодный слой воды температура газа в ампуле уменьшится. Значит, можно подобрать такие параметры, чтобы объем колпачка уменьшился настолько, что сила тяжести стала бы больше силы Архимеда, и ампула начала бы двигаться вниз. При попадании ампулы в нижний горячий слой воды температура газа в ампуле увеличится. И наоборот, можно подобрать такие параметры, чтобы объем колпачка увеличился настолько, что сила Архимеда стала бы больше силы тяжести, и ампула начала бы двигаться вверх, снова попадая в холодный слой. Таким образом, можно найти такие условия, что ампула будет совершать колебательные движения между верхней и нижней границами воды за счет градиента температур.

Найдем эти условия аналитически. Как уже было сказано, характер движения ампулы определяется ее объемом. Зависимость объема от высоты можно получить из уравнения состояния газа:

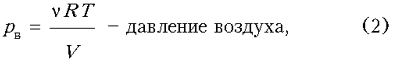
n – количество газа, R – универсальная газовая постоянная, Т – температура, pсп = AemT – давление насыщенного пара спирта, A=0,0011 Па, m=0,053 K–1.

Тогда можно записать зависимость объема от высоты.

Из уравнения

следует, что

где p0 – атмосферное давление, k – коэффициент упругости колпачка, V0 – начальный объем колпачка, hст – высота столба воды.

Определим условия, при которых ампула будет совершать колебательные движения вверх-вниз.

Первое условие: сила тяжести должна быть больше силы Архимеда, когда ампула находится у верхней границы воды, чтобы она начала опускаться:

где T2 – температура воды у поверхности.

Второе условие: сила Архимеда должна быть больше силы тяжести, когда ампула находится у дна сосуда, чтобы она начала подниматься:

где T1 – температура воды у дна цилиндра.

Итак, когда мы знаем эти условия, мы можем подобрать необходимые параметры и поставить эксперимент. При его постановке мы столкнулись с проблемой: конвекция в воде происходила очень быстро, т.е. холодная вода оказывалась снизу, а горячая – сверху за короткое время по сравнению со временем, необходимым для процесса. Это происходило потому, что плотность холодной воды больше плотности горячей. Для разрешения проблемы мы увеличили плотность горячей воды, немного подсолив ее. Теперь перейдем к эксперименту. Мы помещали ампулу на некоторую высоту в воду, удерживали некоторое время и отпускали. Она действительно начинала совершать колебательные движения, причем эти колебания имели следующий характер: ампула опускалась на дно сосуда, покоилась там некоторое время, затем поднималась вверх, достигала верхней границы воды, покоилась там некоторое время, затем опять опускалась вниз и т.д., т.е. колебания не были затухающими. Этот процесс продолжался в течение 3–5 мин, пока температура воды существенно не изменилась. Затем мы исследовали зависимость характера колебаний от силы вязкого трения. Для этого мы прикрепили к ампуле небольшой плоский ободок, тем самым увеличив эту силу. И получили очень интересные результаты: колебания стали затухать в течение 30–50 с (в зависимости от начальных параметров). Чтобы убедиться в том, что это затухание происходит не из-за изменения температуры воды, а именно из-за увеличения силы трения, мы провели дополнительный эксперимент: налили воду в сосуд так, как сказано в условии, опустили туда ампулу, колебания начались, мы сняли экспериментальную зависимость высоты ампулы от времени и, когда колебания прекратились, вытащили ампулу и повторили все действия еще раз в той же воде, получив еще одну экспериментальную зависимость. Если бы распределение температуры воды в течение времени первого процесса изменилось значительно, то результаты существенно отличались бы друг от друга, но они почти совпадали. Значит, температура воды за время процесса изменилась незначительно. Итак, мы получили, что колебания ампулы могут быть затухающими, но могут и не затухать, пока температура в каждой точке воды существенно не изменилась.

Опишем движение ампулы теоретически и найдем причины таких колебаний. Для этого, как и в любой модели, сделаем несколько приближений. Во-первых, будем считать, что за время процесса температура в каждой точке воды не изменилась. Как было сказано ранее, мы проверили экспериментально, что в течение 1–2 мин это изменение очень мало и не оказывает существенного влияния на движение ампулы. Также важно отметить, что температура газа в ампуле устанавливается равной температуре снаружи не сразу, т.к. необходимо время для нагревания самой ампулы и колпачка. Мы учтем это, но упростим: будем считать, что температура газа в какой- то момент времени равна температуре, которая была снаружи некоторое время t0 назад, т.е.:

Итак, для описания движения ампулы составим уравнение ее движения:

где vh – скорость ампулы на высоте h, m – ее масса. На ампулу действуют сила тяжести, сила Архимеда и сила вязкого трения (будем считать, что она прямо пропорциональна скорости ампулы). Объем тела в этом уравнении заменим полученным ранее выражением (4):

Мы получили дифференциальное уравнение, которое не имеет аналитического решения. Поэтому мы решили его численно на компьютере, написав программу. Принцип ее работы следующий: задаем начальную высоту и начальную скорость; подставив их в уравнение, находим начальное ускорение; считаем, что в течение очень малого промежутка времени Dt ампула движется равноускоренно с этим ускорением, таким образом, находим высоту подъема ампулы и ее скорость через время Dt и, опять подставляя их в уравнение, находим новое ускорение ампулы и т.д. С помощью этой программы нами были получены теоретические графики зависимости высоты ампулы от времени для параметров, при которых проводились эксперименты (рис. 1, 2). Как видите, получено хорошее согласие теоретических и экспериментальных результатов в обоих случаях.


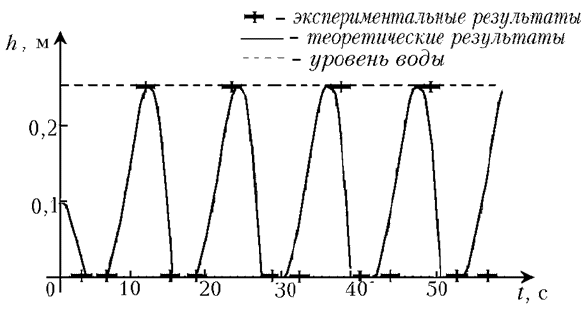
Р РёСЃ. 1.

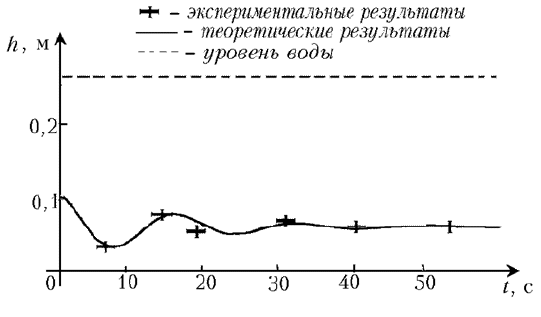
Р РёСЃ. 2.

Теперь ответим на вопрос: почему же появляются такие различия в характере колебаний?

Для этого в нашу программу были внесены изменения: мы убрали силу трения и, на всякий случай, запаздывание температуры, т.е. считали, что температура газа в ампуле устанавливается равной температуре снаружи мгновенно. Результат в этом случае достаточно прост: амплитуда с течением времени не изменяется. Затем мы включили силу трения. И также получили ожидаемый результат: в этом случае амплитуда уменьшается с течением времени. После этого мы снова убрали силу трения, но включили запаздывание температуры. И получили очень интересный результат: в этом случае амплитуда с течением времени увеличивается (рис. 3).


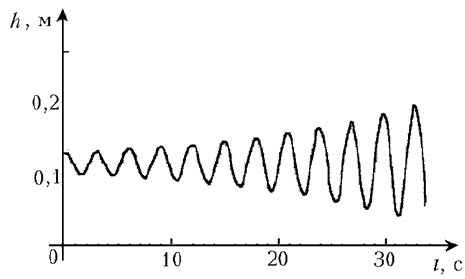
Р РёСЃ. 3.

Это можно объяснить. Рассмотрим момент, когда ампула находится на высоте h0, где результирующая сила, действующая на нее, была бы равна нулю, если бы запаздывания температуры не было (рис. 4). Но т.к. есть запаздывание температуры, то в этот момент температура газа в ампуле равна температуре воды на высоте, где ампула находилась время t0 назад, т.е. температура газа внутри ампулы больше температуры воды на данной высоте h0. А значит, и объем колпачка в случае с запаздыванием больше объема, который был бы на данной высоте, если бы запаздывания температуры не было. Следовательно, в этом случае (с запаздыванием) результирующая сила, действующая на ампулу, не равна нулю и направлена вверх. Следовательно, в этом случае до следующей полной остановки ампула пройдет большее расстояние и остановится выше, чем в случае, если бы запаздывания не было. Движение ампулы вниз рассматривается аналогично. Таким образом, амплитуда колебаний будет увеличиваться с течением времени. Итак, если теперь включить в программу и силу трения, и запаздывание температуры, то мы можем получить различные случаи в зависимости от соотношения коэффициента вязкого трения и времени запаздывания t0: амплитуда может увеличиваться, но может и уменьшаться. Именно этим и объясняется то, что, увеличив коэффициент трения в нашем эксперименте, мы получили затухающие колебания.


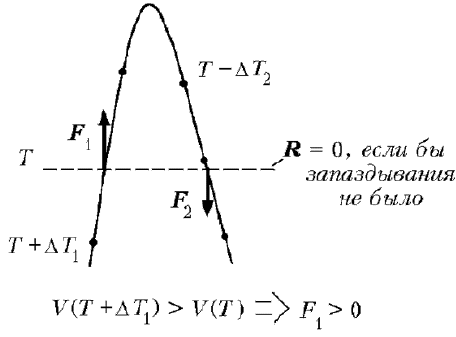
Р РёСЃ. 4.

Итак, подведем итоги: мы описали процесс качественно; нашли условия, необходимые для его наблюдения; провели эксперименты и получили различный характер движения ампулы; создали модель этого процесса и с ее помощью объяснили полученные различия; получили теоретические зависимости и, сравнив их с экспериментальными, получили хорошее согласие, что говорит том, что основная суть физического процесса была понята нами правильно.

Николай Булатов,
11-й класс, СУНЦ УрГУ, г. Екатеринбург.
Материал прислала Инишева Ольга Викторовна,
заместитель директора СУНЦ УрГУ по научной работе

TopList