Продолжение. См. № 48/04
8. Серебряная и пластмассовая ложки
1. Предварительные замечания
РљРѕРіРґР° СЏ помешиваю горячий кофе серебряной ложечкой, СЏ чувствую, как быстро нагревается её конец Сѓ меня РІ СЂСѓРєРµ. Если же вместо серебряной взять пластмассовую ложечку, её конец остаётся холодным. Отсюда можно сделать вывод, что серебро РїСЂРѕРІРѕРґРёС‚ тепло лучше, чем пластмасса. РР· повседневного опыта СЏ прихожу Рє выводу, что РІСЃРµ вещества можно разделить РЅР° РґРІР° класса: те, которые РїСЂРѕРІРѕРґСЏС‚ тепло хорошо, Рё те, которые РїСЂРѕРІРѕРґСЏС‚ её плохо. Рзвестно, что металлы (серебро, медь или алюминий) являются хорошими проводниками тепла Рё электрического тока, Р° вещества типа стекла или пластмассы являются плохими проводниками Рё того Рё РґСЂСѓРіРѕРіРѕ. Поэтому можно ожидать, что есть что-то общее РІ том, как вещества РїСЂРѕРІРѕРґСЏС‚ тепло Рё электрический ток. Ниже РјС‹ убедимся, что так РѕРЅРѕ Рё есть.
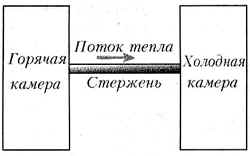
Чтобы СЏСЃРЅРѕ понять, что РјС‹ подразумеваем РїРѕРґ теплопроводностью, рассмотрим простой пример (СЂРёСЃ. 8-1). Стержень РёР· некоторого вещества, например, серебра или стекла, соединяет РґРІРµ камеры, РѕРґРЅР° РёР· которых горячая, Р° другая – холодная. Если измерить температуру вдоль стержня, то можно обнаружить, что стержень сильно нагрет РЅР° РѕРґРЅРѕРј конце Рё холодный РЅР° РґСЂСѓРіРѕРј, Р° вдоль стержня температура постепенно уменьшается. Ртот пример является идеализацией примера СЃ ложечкой РІ чашке кофе. Рнергия РІ форме тепла непрерывно переносится РѕС‚ горячей камеры вдоль стержня Рє холодной камере.

Рис. 8-1. Тепловая энергия переносится по стержню от его горячего конца к холодному
Вопрос. Откуда нам известно, что энергия действительно переносится указанным способом?
Ответ. Если заменить холодную камеру куском льда, то лёд начнёт постепенно таять за счёт тепловой энергии, получаемой от горячей камеры.
Проделаем теперь ещё один эксперимент: соединим два куска льда стержнем, предварительно охладив его до температуры льда. В этом случае не наблюдается никакого потока тепла через стержень, т.к. куски льда не тают. При этом во всех приводимых рассуждениях я предполагаю, что из окружающего пространство в куски льда и стержень никакое тепло не поступает.
Рти РґРІР° эксперимента РїСЂРёРІРѕРґСЏС‚ Рє важному выводу: тепловая энергия передаётся стержнем только РІ том случае, если его концы имеют разную температуру. Рменно разность температур заставляет тепло перемещаться вдоль стержня.
Проделаем теперь третий эксперимент. Возьмём металлическую ложку Рё, удерживая её РґРІСѓРјСЏ пальцами, опустим РІ стакан СЃ горячим чаем. РћРґРёРЅ конец ложки немедленно нагреется, Рё тепло начнёт медленно распространяться вдоль ложки Рє холодному концу. Р’ этом можно убедиться, последовательно притрагиваясь Рє ложке РІ разных местах. Требуется нескольких секунд, РёРЅРѕРіРґР° даже РјРёРЅСѓС‚ (РІ зависимости РѕС‚ вещества, РёР· которого сделана ложка), чтобы почувствовать изменения температуры вдоль ложки. Рту ситуацию можно изобразить графически (СЂРёСЃ. 8-2): так изменяется температура РІ разных точках ложки РІ разные моменты времени. Кривые 1–4 показывают температуру вдоль ложки РІ начальный Рё три последующих момента. Резкий скачок температуры, возникший РЅР° РѕРґРЅРѕРј конце, затем медленно распространяется вдоль ложки.
Резюмируем результат трёх экспериментов РїРѕ распространению тепла вдоль стержня РёР· определённого вещества: чтобы РІРѕР·РЅРёРє поток тепла, необходима разность температур между РґРІСѓРјСЏ точками вдоль стержня; поток тепла распространяется РѕС‚ горячего конца Рє холодному; его распространение довольно медленное. Попробуем теперь объяснить эти факты, основываясь РЅР° модели твёрдого тела, которую РјС‹ развили РІ предыдущей главе. Нам потребуются РґРІРµ новые идеи. Нужно ввести меру того, сколько тепловой энергии должно поглотить вещество, чтобы изменилась его температура, Рё предложить СЃРїРѕСЃРѕР± учёта столкновений между электронами Рё фононами. Рто станет предметом обсуждения РІ РґРІСѓС… следующих параграфах.
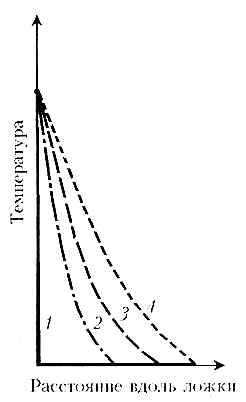
Р РёСЃ. 8-2. Рзменение температуры вдоль металлической ложки РІ четыре последовательных момента времени после того, как РѕРґРёРЅ конец ложки погрузили РІ горячий чай. Кривая 1 показывает ситуацию РІ момент времени 1: конец ложки нагрет, РЅРѕ остальная часть ещё РЅРµ получила «сообщения» РѕР± этом. Кривые 2, 3, 4 показывают, как тепло медленно распространяется вдоль ложки
2. Удельная теплоёмкость
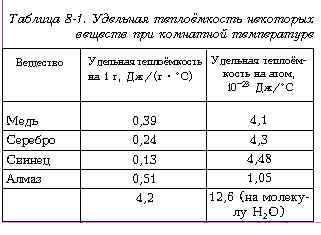
РљРѕРіРґР° определённое количество энергии РІ форме тепла передаётся РєСѓСЃРєСѓ вещества, этот РєСѓСЃРѕРє становится горячее. Если повторить этот эксперимент СЃ одинаковыми РїРѕ массе кусками разных веществ, то обнаруживается, что РёС… температура повышается РЅР° разную величину, несмотря РЅР° то, что количество поступившей РІ каждый РєСѓСЃРѕРє тепловой энергии одинаково. Можно обратить утверждение: чтобы поднять температуру разных РєСѓСЃРєРѕРІ вещества одинаковой массы РЅР° РѕРґРЅСѓ Рё ту же величину, требуется разное количество тепловой энергии. Р’ табл. 8-1 приведены значения того количества тепловой энергии, которое необходимо затратить, чтобы нагреть грамм разных веществ РѕС‚ 20°С РґРѕ 21°С. Рта величина называется удельной теплоёмкостью РЅР° грамм вещества. Поскольку РёР· РґСЂСѓРіРёС… экспериментов известно число атомов РІ 1 Рі любого вещества, можно вычислить также удельную теплоёмкость РЅР° РѕРґРёРЅ атом (СЃРј. второй столбец РІ табл. 8-1). РР· таблицы РІРёРґРЅРѕ, что удельная теплоёмкость РЅР° грамм разная для разных веществ, РІ то время как удельная теплоёмкость РЅР° атом примерно одинакова для первых трёх веществ Рё меньше для алмаза. РњС‹ вернёмся Рє обсуждению этого РІРѕРїСЂРѕСЃР°, Р° сейчас посмотрим, что РїСЂРѕРёСЃС…РѕРґРёС‚ СЃ электронами Рё фононами РІ твёрдом теле, РєРѕРіРґР° РѕРЅРё получают дополнительную тепловую энергию.
Начнём СЃ тепловой энергии, сосредоточенной РІ фононах, представляющих СЃРѕР±РѕР№ колебания РёРѕРЅРѕРІ (атомов) кристаллической решётки. Предположим, что кристалл находится РїСЂРё температуре 20 °С (293 Рљ). Будем называть это комнатной температурой Рё обозначать символом Рў. Р’СЃРїРѕРјРЅРёРј, что существует максимальная частота фононов fР”. Если эта частота такова, что энергия kT РјРЅРѕРіРѕ больше энергии фононов hfР”, то РЅР° основании статистических законов для фононов находим, что средняя тепловая энергия, приходящаяся РЅР° РѕРґРёРЅ атом, равна 3kT. РЎРёРјРІРѕР» k РІ этих соотношениях обозначает постоянную Больцмана – РјРёСЂРѕРІСѓСЋ постоянную, равную 1,38•10–23 Дж/Рљ. РџСЂРё температуре, которая РЅР° РѕРґРёРЅ градус выше комнатной, тепловая энергия, приходящаяся РЅР° РѕРґРёРЅ атом, равна 3k(Рў + 1). Таким образом, приходящаяся РЅР° каждый атом дополнительная энергия, необходимая для того, чтобы повысить температуру РЅР° РѕРґРёРЅ градус (РјС‹ назвали эту энергию удельной теплоёмкостью РЅР° атом) равна разности этих РґРІСѓС… энергий, С‚.Рµ. 3k, или численно 4,14•10–23 Дж/Рљ. Ртак, удельная теплоёмкость РЅР° атом должна иметь это значение для всех веществ. РР· табл. 8-1 следует, что это утверждение приближённо верно для меди, серебра Рё свинца, РЅРѕ плохо выполняется для алмаза. Причина РІ том, что Сѓ алмаза частота fР” РјРЅРѕРіРѕ выше, чем аналогичная частота для трёх металлов, Рё чтобы kT стало РјРЅРѕРіРѕ больше hfР”, нужно перейти Рє значительно более высоким температурам. Если это условие РЅРµ выполнено, то статистическая физика фононов утверждает, что удельная теплоёмкость уменьшается, стремясь Рє нулю РїСЂРё приближении температуры Рє абсолютному нулю. Р’СЃРµ эти предсказания подтверждаются экспериментами.
Р’РЅРѕРІСЊ обращаясь Рє табл. 8-1, РІРёРґРёРј, что удельная теплоёмкость РЅР° атом для трёх металлов РЅР° самом деле слегка больше, чем 3k, определяемая вкладом фононов. Ртот избыток частично обязан СЃРІРѕРёРј происхождением наличию РІ металлах электронов проводимости, которые РјРѕРіСѓС‚ получать тепловую энергию Рё переходить РІ соседние незанятые квантовые состояния, РІРЅРѕСЃСЏ, таким образом, вклад РІ удельную теплоёмкость. Оценим этот вклад.
Вопрос. В диэлектриках вклад электронов в удельную теплоёмкость отсутствует или очень мала. Почему?
Ответ. В диэлектриках вблизи квантовых состояний, занятых электронами, отсутствуют незанятые квантовые состояния, в которые электроны могли бы перейти, поглощая тепловую энергию.
Рассмотрим решётку металла СЃ N атомами РІ 1 СЃРј3. Как РјС‹ видели, тепловые колебания определяют фононную часть удельной теплоёмкости: CСЂ=3Nk. Рндекс «р» напоминает, что этот вклад определяется решёткой. Предположим теперь, что РёР· каждого атома освобождается РѕРґРёРЅ электрон; энергии всех этих электронов образуют поверхность Ферми. РџСЂРё температуре 0 Рљ электроны занимают РІСЃРµ квантовые состояния вплоть РґРѕ состояния максимальной энергии, называемой энергией Ферми EF. Рта энергия примерно РІ тысячу раз больше тепловой энергии, приходящейся РЅР° РѕРґРёРЅ атом РїСЂРё комнатной температуре. РџСЂРё температуре Рў дополнительная тепловая энергия, которую может поглотить электрон, РїРѕСЂСЏРґРєР° kT, Рё это составляет малую долю энергии Ферми. Как показано РЅР° СЂРёСЃ. 6-18 [СЃРј. в„– 36/04. – Ред.], отсюда следует, что РІ незанятые состояния более высокой энергии РјРѕРіСѓС‚ переходить только те электроны, энергии которых меньше энергии Ферми примерно РЅР° величину kT, Рё РѕРЅРё оставляют вместо себя незанятые состояния, эквивалентные дыркам. Число таких электронов Рё дырок есть доля (kT/EF) РёС… полного числа N. Каждый РёР· РЅРёС… имеет РІ среднем энергию kT, так что полная тепловая энергия электронов Рё дырок равна РёС… числу N(kT/EF), умноженному РЅР° kT, С‚.Рµ. равна Nk2T2/EF.
Если теперь нагреть кристалл от температуры Т до температуры Т + 1, то энергия электронов и дырок увеличится до Nk2(T + 1)2/EF. Разность этих энергий как раз равна энергии, которую нужно передать электронам и дыркам в кристалле объёмом в 1 см3, чтобы поднять температуру на один градус, т.е. это есть электронная удельная теплоёмкость, которую можно обозначить Се:
Се = Nk2(Т + 1)2/EF – Nk2T2/EF.
Приближённо это равно Се = 2Nk2Т/EF (можно пренебречь единицей по сравнению с Т).
Теперь мы знаем, сколько энергии нужно передать фононам, а сколько – электронам и дыркам, чтобы повысить температуру кристалла на один градус. Удельная теплоёмкость кристалла как целого равна сумме удельных теплоёмкостей решётки и электронов. Можно найти относительный вклад от этих двух источников, вычислив отношение
![]()
Рнергия Ферми РІ тысячу раз больше тепловой энергии, так что электронная удельная теплоёмкость составляет тысячную долю РѕС‚ фононной. Отсюда следует, что Сѓ металлов РїСЂРё комнатной температуре основная доля энергии, необходимой для нагреваения кристалла, передаётся фононам Рё только очень малая часть – электронам проводимости. Р’ диэлектрике или полупроводнике вообще нет свободных электронов (или РёС… число пренебрежимо мало), так что практически РІСЃСЏ энергия РїСЂРё нагревании передаётся фононам.
3. Средняя длина свободного пробега
Вернёмся Рє стержню РЅР° СЂРёСЃ. 8-1. Рнергия РІ форме тепла непрерывно перетекает РѕС‚ его горячего конца Рє холодному. Попробуем описать это явление РЅР° языке электронов, дырок Рё фононов. Рти объекты обладают тепловой энергией Рё поэтому ответственны Р·Р° её перенос РїРѕ стержню.
Рассмотрим сначала стержень из диэлектрика, в котором носителями тепловой энергии являются только фононы, а свободных электронов просто нет. Ниже мы увидим, что результат, полученный только для фононов, применим с определёнными оговорками к электронам и дыркам. На рис. 8-3 показан стержень. Стрелки представляют фононы с одной из многих возможных частот, которые летают во всех возможных направлениях со скоростью, равной скорости звука в образце. Плотность, т.е. число фононов в единице объёма, постепенно уменьшается при переходе от горячего конца к холодному. То же самое происходит с фононами других частот, так что результаты, которые мы получим для фононов одной частоты, будут пригодны для всех фононов.
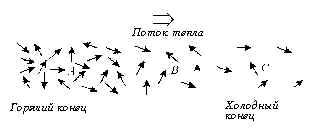
Р РёСЃ. 8-3. Р’ стержне, РїРѕ которому распространяется тепло, имеются фононы всех частот, РЅРѕ показаны только фононы РѕРґРЅРѕР№ частоты. Каждая стрелка изображает фонон, распространяющийся РІ указанном направлении. Плотность фононов, С‚.Рµ. РёС… число РІ единице объёма, постепенно уменьшается РѕС‚ горячего конца стержня Рє холодному. Рто РІ конце концов РїСЂРёРІРѕРґРёС‚ Рє возникновению потока тепла РѕС‚ горячего конца Рє холодному
Вопрос. Почему плотность фононов при более высокой температуре больше?
Ответ. Чем выше температура, тем больше тепловой энергии РїСЂРѕС…РѕРґРёС‚ через данное сечение стержня. Рта энергия содержится РІ фононах, поэтому РІ данном сечении число фононов увеличивается.
Рассмотрим фонон вблизи горячего
конца стержня в области А. Прежде чем
столкнуться с другим фононом, он пролетит
определённое расстояние. Предположим, что
соударение происходит в области В.
В результате в силу закона сохранения энергии
фононы в области В превращаются в фононы
большей энергии, полная энергия которых равна
энергии начальных фононов. Раз увеличилась
энергия, следовательно, в области соударения
стало больше фононов, чем это предписывается
значением температуры РІ этой области. Рти
избыточные фононы продолжают соударяться со
следующими фононами, так что та же история
случается и дальше вдоль стержня. Одновременно в
области В существует и противоположно
направленный поток тепловой энергии за счёт
фононов, прибывающих из области типа С, ближе
к холодному концу стержня. Суммарный поток
энергии равен разности двух потоков.
Расстояние, которое пролетает фонон перед соударением, для каждого своё. Чтобы упростить рассуждения, предположим, что существует некоторое среднее расстояние между двумя последовательными соударениями. Назовём его средней длиной свободного пробега и обозначим l. Смысл этой величины в том, что в среднем фонон переносит энергию на расстояние l вдоль стержня, до того как испытает соударение и передаст энергию другим фононам, а те продолжат процесс. Некоторые экспериментальные данные о величине l приведены в табл. 8-2.
Рлектроны Рё дырки РІ металле испытывают соударения как СЃ фононами, так Рё СЃ атомами примесей РІ случае сплавов. Для РЅРёС… также существует понятие средней длины СЃРІРѕР±РѕРґРЅРѕРіРѕ пробега. Некоторые экспериментальные данные приведены РІ табл. 8-2.
Таблица 8-2. Средняя длина пробега частиц при комнатной температуре
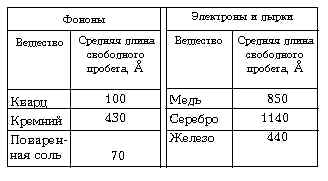
Расстояние между соседними атомами РІ твёрдом теле составляет несколько ангстрем (1 A = 10–10 Рј). Таким образом, РІРёРґРЅРѕ, что РІСЃРµ указанные частицы пролетают перед соударениями довольно большие расстояния (РїРѕ сравнению СЃ межатомными). Если Р±С‹ это были частицы РІ обычном смысле, то можно было Р±С‹ ожидать, что средняя длина СЃРІРѕР±РѕРґРЅРѕРіРѕ пробега РїРѕСЂСЏРґРєР° межатомных расстояний. Рменно квантовые свойства частиц ответственны Р·Р° столь большие средние длины СЃРІРѕР±РѕРґРЅРѕРіРѕ пробега.