В.Б.ДРОЗДОВ, г. Рязань

Криволинейное равноускоренное движение

Рассмотрим серию физических задач о движении тел вблизи земной поверхности. Пусть скорости тел относительно невелики, тогда мы вправе пренебречь трудноучитываемым сопротивлением воздуха и уж тем более зависимостью ускорения свободного падения от высоты над поверхностью Земли и кривизной этой поверхности. Однако и при этих упрощающих предположениях задачи на криволинейное равноускоренное движение представляют для многих абитуриентов достаточно серьёзную проблему. Для её преодоления необходимо и достаточно учесть следующее.

Во-первых, не надо запоминать массу второстепенных частных кинематических формул. Это и трудно, и нецелесообразно. С одной стороны, их использование без вывода на экзамене неправомерно, а значит, приведёт к снижению оценки. С другой стороны, можно и ошибочно «вспомнить» формулу, перепутав, например, синус с косинусом или плюс с минусом. Нужно знать две основные формулы: для вектора перемещения s и мгновенной скорости в случае произвольного равноускоренного движения:

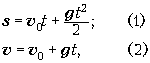
где ₀ – начальная скорость тела, g – ускорение свободного падения.

Во-вторых, нужно твёрдо знать операции с векторами, простейшие тригонометрические формулы, свойства квадратичной функции. При проецировании вектора на ось нерационально из его концов опускать на неё перпендикуляры. Лучше помнить формулу a_x = acos – проекция вектора на ось равна его модулю, умноженному на косинус угла между вектором и осью. Не забудем, что этот угол измеряется «от стрелки до стрелки» и может быть равен от 0° до 180° включительно. Ну а далее помогут тригонометрические формулы приведения. Три простейших случая: параллельность, антипараллельность и перпендикулярность вектора и оси запоминаются сами собой, хотя и следуют из общей формулы.

В-третьих, обязательна тренировка в решении задач: и рассмотрение с карандашом в руках разобранных, и самостоятельное решение задач «домашних». Отметим, что среди задач есть немало объективно трудных.

Если тело брошено из начала координат с начальной скоростью где ₀ под углом к горизонту, то формула (1) в проекциях на оси X и Y соответственно даёт:

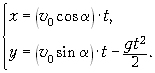         (1' )

При этом дальность полёта тела по горизонтали:

             (3)

Максимальная высота подъёма тела:

             (4)

Время полёта тела

             (5)

Формулы (1' ), (3)–(5) даны для удобства решения задач – они выводятся в школьных учебниках. Переходим к решению задач.

Задача 1. Двое играют в мяч, бросая его друг другу. Какой наибольшей высоты достигает мяч во время игры, если от одного игрока к другому он пролетает за время T = 2 с?

Решение. Формулы (4) и (5) образуют систему двух уравнений с тремя неизвестными: H, ₀, :

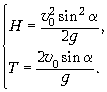
Не будем бесплодно искать третье уравнение: оно не нужно, ибо величину можно рассматривать как единую. Тогда из первого уравнения:

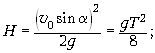Н = 4,9 м.

Очевидно, что определить ₀ и отдельно невозможно, – это и не требуется по условию задачи.

Задача 2 (МФТИ, 1994). С верхней точки шара радиусом R = 54 см, закреплённого на горизонтальной поверхности стола, соскальзывает без начальной скорости и без трения небольшой шарик. На какую максимальную высоту от стола поднимается шарик после упругого удара о стол?

Решение.

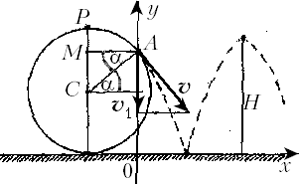
Прежде чем приступить к кинематике, необходимо определить из динамических соображений положение точки отрыва A шарика от шара. В этой точке исчезает сила реакции поверхности шара, и с момента отрыва и до падения ускорение шарика равно g. Проекция вектора g на радиус AC равна нормальной составляющей ускорения, т.е. где – скорость шарика в точке A. Применив закон сохранения энергии для точек P и A, получим:

Но PM = R – Rsin .

Исключая PM и ², находим:

При этом

Вертикальная составляющая скорости тела в точке A равна Она будет увеличиваться в свободном падении и при ударе о плоскость составит ₂ = ₁ + gT, где T – время от отрыва до удара шарика. Его найдём из квадратного уравнения ибо в момент падения тела его ордината равна нулю:

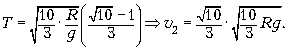
Максимальная высота H подъёма шарика определяется лишь его вертикальной составляющей ₂:

Задача 3. Из шланга, лежащего на земле, под углом  = 45° к горизонту бьёт струя воды с начальной скоростью ₀ = 10 м/с. Площадь сечения отверстия шланга S = 5 см². Определите массу струи, находящейся в воздухе.

Решение. Ясно, что масса струи, вытекающая в единицу времени, равна где  = 10³ кг/м³ – плотность воды. Масса воды в воздухе:

Числовой расчёт даёт m = 7 кг.

Задача 4. Дальность полёта снаряда, летящего по навесной траектории, равна максимальной высоте подъёма H = 1200 м. Найдите максимальную высоту h настильной траектории при этой же дальности полёта.

Решение. Из формул (3) и следует, что дальность полёта тел, брошенных с одной и той же начальной скоростью под углами и к горизонту, равны. Навесной траектории соответствует угол бросания больше 45°, настильной – меньше 45°. В соответствии с условием задачи запишем систему уравнений:

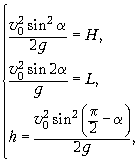
H = L,

которая очевидно упрощается:

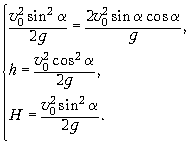
Далее: