17 декабря 2006 Рі. РІ РњРѕСЃРєРѕРІСЃРєРѕРј инженерно-физическом институте (РњРР¤Р) проходила традиционная олимпиада РїРѕ физике памяти профессора РРіРѕСЂСЏ Владимировича Савельева. Р.Р’.Савельев РІ течение РјРЅРѕРіРёС… лет был заведующим кафедрой общей физики РњРР¤Р, РѕРЅ является автором СЂСЏРґР° классических учебников Рё задачников для студентов-физиков. Рти РєРЅРёРіРё используются РІ качестве РѕСЃРЅРѕРІРЅРѕРіРѕ учебника РІ СЂРѕСЃСЃРёР№СЃРєРёС… технических вузах, переведены РЅР° РјРЅРѕРіРёРµ иностранные языки Рё являются настольными книгами молодых физиков РІРѕ всем РјРёСЂРµ.
Олимпиада памяти Р.Р’.Савельева традиционно проводится РІ середине декабря РІ РњРР¤Р. Рта олимпиада является РѕРґРЅРёРј РёР· туров Всероссийской физико-математической олимпиады Федерального агентства РїРѕ атомной энергии (Росатома), которая проводится РІ несколько туров РІ течение всего учебного РіРѕРґР° РІ РњРѕСЃРєРІРµ (РІ РњРР¤Р) Рё СЂСЏРґРµ крупных центров Росатома (Рі. Саров, Рі. Снежинск Рё РґСЂ.) для школьников 11-С… классов. Победители Рё призёры олимпиады Росатома (около 10% участников) получают существенные льготы РїСЂРё зачислении РІ РњРР¤Р. Подробности РѕР± олимпиаде Росатома 2007/2008 СѓС‡.Рі. можно узнать РїРѕ телефону приёмной РєРѕРјРёСЃСЃРёРё РњРР¤Р: (495) 324-84-17 Рё РЅР° сайте приёмной РєРѕРјРёСЃСЃРёРё РњРР¤Р: http://www.priem.mephi.ru.
РќР° олимпиаде памяти Р.Р’.Савельева РІ 2006 Рі. школьникам были предложены пять задач различной степени сложности. Ниже приводится вариант задания олимпиады Рё его РїРѕРґСЂРѕР±РЅРѕРµ решение.
Вариант задания олимпиады
1. Ускорение свободного падения на поверхности некоторой планеты равно g = 16 м/с2, на высоте h = 1000 км от поверхности – g1 = 9 м/с2. Найдите радиус планеты.
Решение
Основная идея решения задачи заключается РІ том, что ускорение СЃРІРѕР±РѕРґРЅРѕРіРѕ падения РЅР° той или РёРЅРѕР№ высоте определяется силой гравитационного притяжения тела Рє планете. Рспользуя закон всемирного тяготения, получаем для ускорения СЃРІРѕР±РѕРґРЅРѕРіРѕ падания РЅР° поверхности планеты Рё РЅР° высоте h РѕС‚ поверхности
![]()
где G – гравитационная постоянная, M и R – масса и радиус планеты. Деля первое уравнение на второе и решая полученное уравнение, находим:
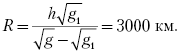
2. РР· точки, находящейся РЅР°
высоте H над землёй, через равные промежутки
времени из состояния покоя падают маленькие
шарики. К тому моменту, когда седьмой шарик
начинает падение, первый падает на землю. Найдите
расстояние между вторым и четвертым шариками в
этот момент. Сопротивлением воздуха пренебречь. 
Решение
За то время, пока первый шарик долетит
до земли, начинают падать ещё шесть шариков (см.
рисунок). Следовательно, время падения первого
шарика на землю равно шести интервалам ![]() t между
падениями любых двух соседних. Поэтому интервал
t между
падениями любых двух соседних. Поэтому интервал ![]() t можно найти,
разделив время падения первого шарика на шесть. А
поскольку время свободного падения тела из
состояния покоя с высоты H составляет
t можно найти,
разделив время падения первого шарика на шесть. А
поскольку время свободного падения тела из
состояния покоя с высоты H составляет ![]() то
то
![]() (1)
(1)
Теперь найдём координаты второго и четвертого шариков в момент падения первого на землю. Для этого заметим, что зависимость координаты х каждого шарика от времени (ось X показана на рисунке) имеет вид
![]() (2)
(2)
где время t отсчитывается от
момента начала падения этого шарика, и что второй
шарик будет двигаться к моменту падения первого
шарика на землю в течение пяти интервалов ![]() t (1), а
четвертый – в течение трёх (см. рисунок).
Подставляя эти значения времени в зависимость (2)
и используя формулу (1), получаем координаты
второго и четвёртого шариков в момент падения
первого на землю:
t (1), Р°
четвертый – в течение трёх (см. рисунок).
Подставляя эти значения времени в зависимость (2)
и используя формулу (1), получаем координаты
второго и четвёртого шариков в момент падения
первого на землю:
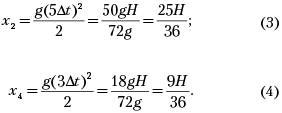
Вычитая теперь координату четвёртого шарика (4) из координаты второго (3), находим расстояние между вторым и четвёртым шариками в момент падения первого на землю:
![]()
3. В сосуде объёмом V0 при температуре T0 и давлении p0 находился воздух, содержащий некоторое количество озона O3. С течением времени озон полностью превратился в молекулярный кислород. Получившийся воздух при температуре T и объёме V оказывает то же самое давление p0, что и первоначальная смесь газов. Найдите первоначальное число молей озона в сосуде.
Решение
Пусть первоначально в сосуде
содержалось ![]() молей
РѕР·РѕРЅР° Рё
молей
РѕР·РѕРЅР° Рё ![]() 1
молей всех остальных газов. Тогда закон Дальтона
для первоначальной смеси газов даёт
1
молей всех остальных газов. Тогда закон Дальтона
для первоначальной смеси газов даёт
![]() (5)
(5)
где R – универсальная газовая постоянная. Поскольку при химической реакции распада озона
2O3 = 3O2, (6)
из каждых двух молекул озона
образуются три молекулы кислорода, то из ![]() молей озона
получается 3
молей озона
получается 3![]() /2
молей кислорода. Поэтому закон Дальтона для
смеси газов после полного распада озона при
новых температуре и объёме даёт
/2
молей кислорода. Поэтому закон Дальтона для
смеси газов после полного распада озона при
новых температуре и объёме даёт
![]() (7)
(7)
Вычитая из формулы (7) формулу (5) и решая полученное уравнение, находим:
![]()
_____________________________________
Сергей Евгеньевич Муравьёв, заместитель заведующего кафедрой теоретической физики РњРР¤Р, Рє.С„.-Рј.РЅ., доцент.
Окончание cм. в № 6/08