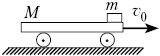Продолжение. См. № 4/08

С.Е.МУРАВЬЁВ, МИФИ, г. Москва

Олимпиада по физике памяти И.В.Савельева

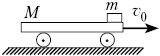4. На передний край тележки массой M, движущейся со скоростью 0 по гладкой горизонтальной поверхности, кладут брусок массой m. Начальная скорость бруска относительно земли равна нулю. Какой должна быть длина тележки, чтобы брусок в дальнейшем не упал с неё? Коэффициент трения между бруском и тележкой равен .

Решение

Брусок и тележка будут двигаться следующим образом. Пока скорость тележки больше скорости бруска (как в начальный момент), на брусок со стороны тележки будет действовать сила трения в направлении её движения, на тележку со стороны бруска – сила трения в противоположном направлении. Поэтому брусок будет разгоняться, тележка – тормозиться. В тот момент, когда скорости тел сравняются (если брусок к этому моменту не упадёт с тележки), сила трения между бруском и тележкой станет равной нулю, и тела будут двигаться вместе с постоянной скоростью. Значит, если брусок к моменту остановки своего движения относительно тележки не упадёт с неё, то он не упадёт и в дальнейшем. Поэтому для нахождения минимальной длины тележки, при которой брусок не упадёт с неё, надо найти перемещение бруска относительно тележки к тому моменту, когда их скорости сравняются, и потребовать, чтобы длина тележки была больше этого перемещения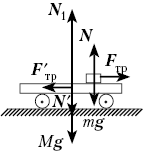. Это18-02.gif (3178 bytes) перемещение можно найти по законам равноускоренного движения, а входящие в них ускорения бруска и тележки – по второму закону Ньютона для этих тел.

На брусок действуют: сила тяжести mg, сила реакции тележки N и трения Fтр, на тележку – сила тяжести Mg, силы реакции со стороны пола N1 и бруска N' и трения F'тр (модули двух последних сил, по третьему закону Ньютона, равны соответственно модулям сил N и Fтр). Силы, действующие на тела, показаны на рисунке. Запись второго закона Ньютона для бруска и тележки в проекциях на горизонтальную ось, направленную вдоль движения тележки, имеет вид (aб и aт – модули ускорений бруска и тележки):

Из уравнений (1) находим ускорения бруска aб и тележки aт:

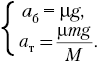
Поскольку ускорения тел постоянны, до момента остановки движение тел является равноускоренным. Поэтому для описания движения тел используем законы равноускоренного движения. Направим ось X системы координат вдоль движения тележки, начало координат поместим в точку, в которой находился брусок в тот момент времени, когда его кладут на тележку; этот момент времени будем считать начальным. Тогда зависимости проекций скорости бруска и тележки на ось Х и координат бруска и тележки от времени определяются уравнениями (координатой тележки считаем координату её начала, т.е. той точки, куда кладут брусок):

  

Из первой и второй формул (1) находим время t1, через которое брусок прекратит перемещаться относительно тележки, т.е. сравняются скорости этих тел

Подставляя время t1 (2) в третье и четвёртое уравнения (1), находим координаты бруска и тележки к тому моменту времени, когда прекращается движение бруска относительно тележки

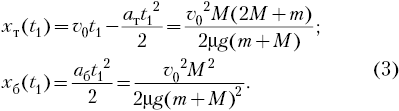
Брусок не упадёт с тележки, если к моменту остановки его движения относительно тележки его перемещение относительно тележки не будет превосходить её длину. Поскольку это перемещение равно разности координат конечной точки тележки и бруска xт(t1) – xб(t1), то условие непадения бруска с тележки есть

xС‚(t1) – xР±(t1) l.     (4)

Подставляя в формулу (4) координаты бруска и тележки (3), найдём, что брусок не упадёт с тележки, если

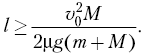         (5)

Возможно и другое решение этой задачи, основанное на законах сохранения импульса и энергии. Приведём и это решение. По закону сохранения импульса найдём скорость бруска и тележки 1 после остановки движения бруска относительно тележки

         (6)

Затем, по теореме об изменении кинетической энергии для бруска и тележки, имеем:

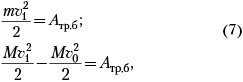
где Aтр.б и Aтр.т – работы силы трения над бруском и тележкой. Поскольку сила трения, действующая на брусок, направлена по его движению, её работа положительна и равна Aтр.б = mgsб, где sб – перемещение бруска относительно земли к тому моменту времени, когда его скорость станет равна 1, т.е. когда прекратится его движение относительно тележки. Для вычисления работы силы трения над тележкой заметим, что тележку в этой задаче нельзя рассматривать как точечное тело, и точка прило жения силы трения перемещается относительно неё. Однако, поскольку ускорение центра масс протяжённого тела определяется суммой действующих на него внешних сил и не зависит от точки их приложения, работа силы трения над тележкой определяется перемещением самой тележки, а не перемещением точки приложения силы трения. Поэтому Aтр.т = –mgsт, (очевидно, что работа силы трения над тележкой отрицательна). Подставляя работы сил трения над бруском Aтр.б и тележкой Aтр.т в уравнения (7) и складывая их, найдём

     (8)

Находя из формул (6), (8) разность перемещений тележки и бруска к моменту остановки движения бруска относительно тележки и требуя, чтобы эта разность не превосходила длину тележки, получим то же самое условие (5) для длины тележки, которое было получено в первом способе решения.

Многие участники олимпиады использовали второй способ решения, который, конечно, является правильным. Однако в целом ряде работ отсутствовали комментарии к вычислению работы силы трения, – школьники сразу п исали закон сохранения энергии в виде (8), используя в качестве разности перемещений тележки и бруска длину тележки sт – sб l и получали правильный ответ. За такое решение (без комментария к вычислению работы силы трения) оценка олимпиадной работы снижалась (при правильном ответе!), поскольку правильным оно оказывалось фактически случайно: если школьник понимал, что работ сил трения две (над бруском и тележкой), что в работу силы трения над бруском и тележкой входят разные перемещения (и мог объяснить, почему), он не мог не прокомментировать эти очень сложные моменты. Отметим, кстати, что в ряде работ (их, к сожалению, было немного) такого рода анализ работы силы трения был выполнен.

Продолжение см. в № 10/08