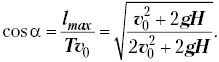При какой наименьшей начальной
скорости камня, брошенного с поверхности Земли,
можно попасть в цель, находящуюся на расстоянии l
по горизонтали и на высоте h по вертикали?
Под каким углом к горизонту надо бросить камень?Задача 9. При какой наименьшей начальной
скорости камня, брошенного с поверхности Земли,
можно попасть в цель, находящуюся на расстоянии l
по горизонтали и на высоте h по вертикали?
Под каким углом к горизонту надо бросить камень?
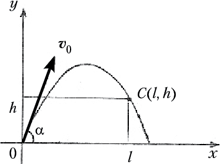
Решение I. Так как траектория тела проходит через точку (l, h), то её координаты удовлетворяют равенству
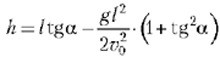
(здесь удобно заменить на 
Отсюда для начальной скорости получаем
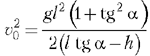
и преобразуем это выражение так:
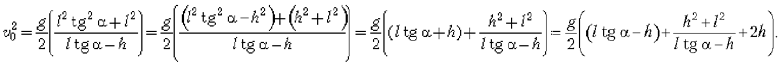
Применим к первым двум слагаемым теорему о среднем арифметическом и среднем геометрическом:
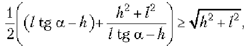
где знак равенства будет при 
т.е. при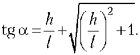 
Значит, 
откуда т.е. 
что будет при
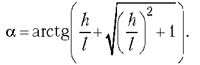
Поэтому траектория камня навесная.
Решение II. Уравнение траектории
камня запишем как квадратное относительно tg 
:
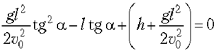
и потребуем неотрицательности его дискриминанта:
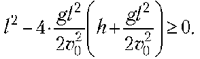
Последнее неравенство легко
преобразовать к квадратному относительно 
Оно, очевидно, верно при 
Следовательно,
чему соответствует нулевой дискриминант и
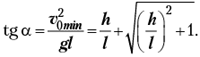
Заметим, что при h = 0 (наземная
цель) = 45°, а 
как и должно быть.
Решение III (общий метод с помощью
производной). Здесь не надо применять
искусственные приёмы. Поэтому самостоятельно
исследуйте функцию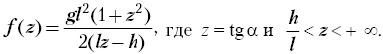 
Задача 10.
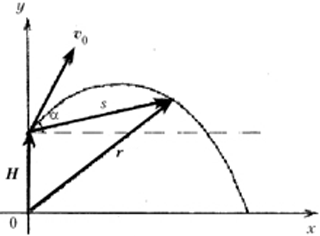
Под каким углом к горизонту надо бросить тело с
башни высотой H, чтобы оно упало как можно
дальше от основания башни? Чему равна наибольшая
дальность полёта тела lmax? Начальная
скорость тела 
0.
Решение I. Спроецируем радиусвектор тела
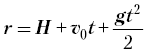
на оси X и Y:
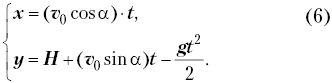
Исключая из системы уравнений (6) время t, получим уравнение траектории тела
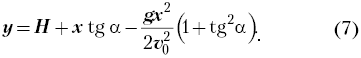
Очевидно, что при y = 0 дальность
полёта l = x. Из соотношения (7) получим для tg следующее
уравнение:
откуда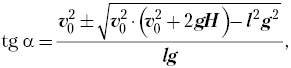 
что
имеет смысл только при неотрицательном
дискриминанте.
Следовательно,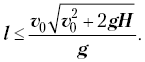 
Поэтому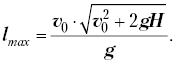 
Наибольшей дальности полёта соответствует
угол бросания такой, что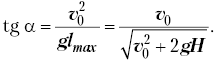 
При H = 0 получаем = 45°, как и должно быть. При H > 0
получаем tg <
1, значит, < 45°.
Решение II. Квадратичную функцию можно использовать и подругому. Запишем решение основной задачи механики для последней точки траектории:
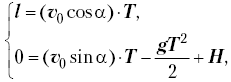
где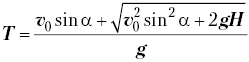 
–
время полёта тела.
(Получается из второго уравнения (6) при y = 0 и t = T.)
Имеем:
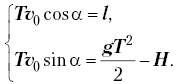
Исключаем sin и cos ,
возводя обе части каждого уравнения в квадрат и
складывая результаты почленно: откуда
Далее преобразуем: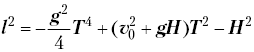 
и исследуем стандартно как
квадратичную функцию относительно T2,
т.е. находим координаты вершины параболы:
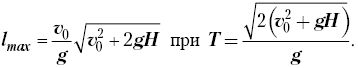
Отсюда нетрудно вычислить и косинус угла бросания:
