Беллур Сиварамия ЧАНДРАСЕКАР

Почему всё вокруг такое, какое оно есть?

Окончание. См. № 2, 4, 6, 8, 10, 12, 16, 18, 20, 22/05

12. Сверхпроводники (окончание)

3. Ключи к разгадке

Объяснение явления сверхпроводимости стало одним из самых впечатляющих достижений физики. Оно представляет собой красивое объединение некоторых идей физики твёрдого тела, уже описанных в этой книге: квантовой механики электронов в твёрдых телах, фононов, природы электропроводности, явлений, связанных с магнитным полем. Перечислим основные факты и отметим, чем они могут быть полезны для объяснения явления. При этом мы не будем следовать истории вопроса и опишем ситуацию так, как она представляется сегодня.

1. В противоположность ферромагнетизму сверхпроводимость – довольно обычное явление: известны сотни сверхпроводников, явление наблюдается у веществ с разнообразной кристаллической структурой и химическим составом. Единственным общим свойством этих веществ, помимо сверхпроводимости, является то, что выше своей температуры перехода они являются металлическими проводниками. Поэтому следует искать объяснение сверхпроводимости в каких-то весьма общих для таких проводников свойствах, которые не зависят от их кристаллической структуры и химического состава.

2. В большинстве случаев температуры перехода ниже 100 К. Напоминаем, что температура есть мера тепловой энергии системы. Средняя кинетическая энергия электронов проводимости в металле, выраженная в единицах температуры, порядка 100 000 К. Таким образом, те энергии, которые соответствуют явлению сверхпроводимости, составляют крохотную долю полной энергии электронов. Возникает образ поиска иголки в стоге сена.

3. Средние энергии фононов близки к энергиям, отвечающим температуре перехода. Поэтому можно полагать, что фононы как-то участвуют в игре. Эта мысль усиливается тем фактом, что температуры переходов разных изотопов одного вещества почти не отличаются друг от друга, а мы знаем, что изотопы отличаются именно своей фононной, а не электронной структурой.

4. Тот факт, что переносчиками сверпроводящего тока являются пары электронов, наводит на мысль, что мы должны искать тот «клей», который связывает электроны в пары.

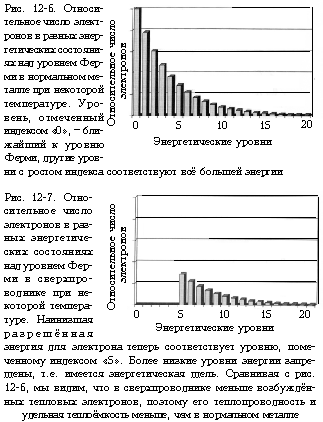
5. Напомним, что теплота в металлах переносится главным образом электронами и дырками, которые благодаря своей тепловой энергии находятся в состояниях, слегка поднятых над энергией Ферми (рис. 12-6). Плохая теплопроводность сверхпроводников означает, что в эти состояния попадает меньше электронов по сравнению с нормальным металлом. Это может произойти, если между энергией Ферми и энергией наинизшего доступного состояния тепловых электронов существует щель (рис. 12-7). Если такая щель возникает в момент перехода в сверхпроводящее состояние, то в этом состоянии оказывается меньше электронов, способных переносить тепловую энергию, по сравнению с числом таких электронов в нормальном металле. В результате сверхпроводник оказывается плохим проводником тепла и обладает малой теплоёмкостью.

Вопрос. Почему у изотопов разная фононная структура?

Ответ. У изотопов разные массы ядер, следовательно, разные атомные массы. Фонон – квант колебательной энергии атома в твёрдом теле, так что эти энергии у атомов с разными массами различны.

4. Куперовские пары и теория БКШ

Физик Леон Купер показал, каким образом определённого типа взаимодействие между электронами может привести к образованию пар связанных электронов, обладающих противоположными значениями импульсов и спинов. Такие пары получили название куперовских пар. Эти пары – очень необычные объекты. Это не просто два электрона, как-то привязанных друг к другу, так что они находятся рядом и движутся как единое целое, т.е. нечто вроде электронной молекулы, состоящей из двух электронов, например как молекула кислорода, состоящая из двух связанных друг с другом атомов. На самом деле два электрона сами по себе не могут образовать связанное состояние, т.к. электрическая сила отталкивания одноимённых зарядов заставит их разлететься в разные стороны. Нужен какой-то посредник, чтобы отталкивание сменилось притяжением. Примером такого посредника является ядро гелия, которое удерживает два электрона на близком расстоянии друг от друга. Это происходит потому, что притяжение к положительно заряженному ядру больше, чем отталкивание электронов друг от друга. Можно сказать, что пара электронов в атоме гелия тесно связана и требуется конечная энергия, чтобы её разорвать. Это та энергия, которая может оторвать электрон от атома гелия, образовав ион.

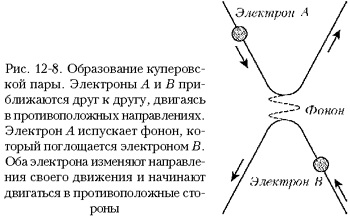
Посредник, объединяющий два электрона в куперовскую пару, – это фонон, квант энергии тепловых колебаний атомов в твёрдом теле. Покажем, как это происходит (рис. 12-8). Два электрона А и В приближаются друг к другу, двигаясь в противоположных направлениях с фермиевской скоростью. Электрон А испускает фонон и начинает двигаться в другом направлении. Электрон В поглощает фонон и изменяет свой импульс на ту же величину, что и А, но направленную в противоположную сторону, так что оба электрона продолжают двигаться, но теперь разлетаются в противоположных направлениях. Пара остается невредимой, но связанной, так сказать, фононом. Это и есть куперовская пара. Такой процесс происходит со всеми парами электронов, двигающихся с противоположно направленными скоростями вблизи всей поверхности Ферми, так что в результате возникает сверхпроводящее состояние. Напомним, что импульс равен массе, умноженной на скорость, поэтому куперовская пара представляет собой два электрона с противоположными импульсами (и следовательно, с нулевым полным импульсом), связанных за счёт испускания и поглощения фонона. Спины двух электронов также противоположно направлены – это проверено на эксперименте и предсказывается теорией.

Вопрос. Каким образом электрон испускает и поглощает фонон?

Ответ. Отрицательный заряд электрона притягивает к себе окружающие положительно заряженные ионы, создавая локальное увеличение давления. Нечто подобное происходит в звуковой волне. Можно говорить об испускании фонона электроном. Через промежуток времени, равный половине периода звуковой волны, сжатие переходит в локальное расширение кристаллической решётки. Если в этот момент рядом окажется второй электрон, он притягивает (за счёт электрических сил) ионы к исходным положениям, что соответствует поглощению фонона.

Итак, мы представляем, как образуются куперовские пары за счёт посредничества фононов. Но происходит не просто образование пар. Оказывается, что энергия электронов в такой паре меньше, чем энергия этих же электронов, движущихся независимо. Когда электрон А создаёт и испускает фонон, он тянет к себе окружающие соседние ионы за счёт электрической силы притяжения между отрицательным зарядом электрона и положительным зарядом иона. Напомним, что фонон – это волна сжатия в твёрдом теле. Поэтому потенциальная энергия электрона меньше, чем она была бы, если бы ионы остались в невозмущённых положениях. Электрон В, приходящий в это место через половину периода фононной волны, «видит» эти ионы на большем расстоянии от себя, чем они были бы без учёта расширения решётки. Поэтому энергия электрона В возрастает. Однако это возрастание меньше, чем уменьшение энергии электрона А. В итоге энергия куперовской пары меньше, чем сумма энергий независимо движущихся электронов. Разность между этими энергиями и есть энергия связи куперовской пары. Чтобы разрушить пару, нужно затратить эту энергию. Мы описали образование куперовских пар. В сверхпроводнике все электроны вблизи поверхности Ферми «спариваются» таким образом при абсолютном нуле температуры. Следует заметить, что образование пары требует двух электронов, которые переходят из начального состояния в конечную пару состояний за счёт испускания и поглощения фонона. Но это возможно только в том случае, если конечная пара состояний свободна, не занята другими электронами. Напомним, что электроны – фермионы, так что в заданном состоянии не может быть более одного электрона.

Из последнего замечания вытекает, что образование куперовских пар зависит от того, что делают все другие электроны. Имеется сильная корреляция между куперовскими парами, они не являются независимыми объектами. Приведём грубую аналогию: электроны в нормальном металле похожи на молекулы газа, все они движутся независимо. Электроны в сверхпроводнике похожи на молекулы в кристалле. Все эти молекулы сильно коррелированы друг с другом, так что кристалл может двигаться только как единое целое, а не как собрание независимых молекул. Точно так же, как говорят о конденсации газа молекул с образованием кристалла, можно говорить и о конденсации электронов в сверхпроводнике в новое состояние – сверхпроводящее. Аналогия очень грубая: молекулы в кристалле конденсируются в упорядоченное состояние в отношении своих положений, чего не происходит в сверхпроводнике. Электроны в сверхпроводнике конденсируются в упорядоченное состояние по отношению к своим импульсам. Но в аналогии есть ещё нечто общее. Атомы газа обладают импульсами, т.к. они движутся, в то время как атомы в кристалле неподвижны (если не считать тепловых колебаний) и их импульс равен нулю. Электроны в нормальном металле также движутся с ненулевыми импульсами, в то время как каждая куперовская пара в сверхпроводнике имеет нулевой импульс и, по существу, покоится. Кристалл может двигаться только как единое целое, и каждая молекула в нём совершает то же движение, что и весь кристалл. Одна из молекул может иметь другую скорость, только если её вытеснили из кристалла, а это требует определённого количества энергии. Аналогично, все куперовские пары в конденсированном состоянии движутся как единое целое и, чтобы выбить из пары отдельный электрон, нужно затратить энергию, равную энергии связи пары.

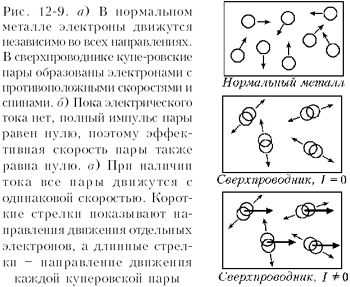
На рис. 12-9 показано, в чём состоит разница между нормальным и сверхпроводящим состояниями металла. Разглядывая рисунок, представьте, что отдельные электроны во всех случаях разлетаются в разные стороны, но куперовские пары либо неподвижны (нулевой ток), либо имеют общую (с током) скорость. В нормальном металле нужно в принципе проследить за путём каждого электрона, чтобы понять поведение металла. В сверхпроводнике достаточно знать поведение всего лишь одной куперовской пары – все остальные ведут себя точно так же.

Теперь можно понять, почему электрический ток в сверхпроводнике течёт, не испытывая сопротивления. Ток переносится куперовскими парами, движущимися с одинаковой скоростью. Электрическое сопротивление возникает в результате рассеяния друг на друге независимо движущихся электронов. Если конденсату куперовских пар передаётся некоторая минимальная энергия, то из него выбрасываются такие свободные электроны. Если электрический ток достаточно большой, то необходимую энергию можно получить за счёт кинетической энергии движения пар. В этом случае энергия будет затрачена на разрушение пар, после чего восстановится нормальное сопротивление. Таким образом, становится понятным, почему ток в сверхпроводнике не может превышать некоторое максимальное значение, называемое критическим током. По достижении этого тока сверхпроводимость разрушается и металл становится нормальным.

Описанная выше картина сверхпроводимости была предложена физиками Джоном Бардином, Леоном Купером и Робертом Шриффером и стала известной как теория БКШ. Эти учёные и их последователи показали, что детальная разработка следствий такой картины объясняет все наблюдаемые свойства сверхпроводников. Теория БКШ явилась одним из величайших достижений квантово-механического описания природы. Первоначально она была разработана для того, чтобы показать, каким образом огромное число электронов в металле может влиять друг на друга за счёт обмена фононами и образовывать сверхпроводящее состояние. Но значение теории БКШ много больше, т.к. она показывает, как следует рассматривать взаимодействующие друг с другом фермионы. Теорию БКШ использовали, например, для объяснения свойств атомных ядер, в которых фермионами являются протоны и нейтроны, и ряда астрономических объектов, называемых нейтронными звёздами, которые состоят из очень плотно упакованных нейтронов.

5. Джозефсоновские переходы

Физик Брайан Джозефсон, использовав теорию БКШ, предсказал явление, которое РІСЃРєРѕСЂРµ действительно было обнаружено Рё получило его РёРјСЏ. Пусть РґРІР° сверхпроводника Рђ Рё Р’ разделены тонкой изолирующей прослойкой РЎ (СЂРёСЃ. 12-10), образуя контакт. Рљ образцам Рђ Рё Р’ подключена батарея, так что Рє РЅРёРј приложено напряжение U. Прослойка РЎ достаточно тонкая, Рё через неё может протекать определённый, пусть Рё маленький, ток. Если РІСЃСЏ остальная часть установки (РЅРµ показанная РЅР° СЂРёСЃСѓРЅРєРµ) собрана должным образом, то обнаруживается, что контакт испускает фотоны (электромагнитные волны) частотой  f = 2eU/h, РіРґРµ Рµ – заряд электрона, Р° h – постоянная Планка. РџСЂРё заданном напряжении частота  f  зависит только РѕС‚ РґРІСѓС… универсальных констант Рё РЅРµ зависит РѕС‚ конкретных свойств используемых сверхпроводников. Это весьма примечательный результат! Явление следует исключительно РёР· самого факта существования куперовских пар (отсюда множитель 2Рµ РІ формуле для частоты) Рё законов квантовой механики (отсюда постоянная Планка h)!

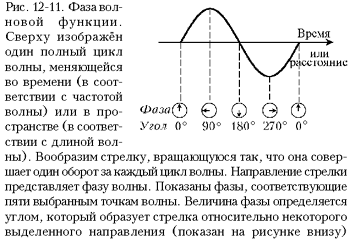
Возникновение эффекта Джозефсона можно понять, вспомнив некоторые основные принципы квантовой механики. Сверхпроводящее состояние обусловлено существованием куперовских пар с нулевым импульсом (когда тока нет) или некоторым ненулевым, но одинаковым для всех пар (когда течёт сверхпроводящий ток конечной величины). Такое состояние можно описать волновой функцией. Сейчас нам не важно, какова точная форма этой функции. Важно, что у этой функции есть часть, определяющая, чему равна энергия и скорость (или, эквивалентно, частота и длина волны) каждой куперовской пары. Обе указанные величины определяют осцилляции волновой функции во времени (частота) и в пространстве (длина волны). Оба осциллирующих свойства можно объединить в единую величину, которая называется фазой и представляет попросту угол (рис. 12-11). Фаза обладает следующими свойствами, вытекающими из того, что она есть часть волновой функции:

1. Частота осцилляций f непосредственно связана с энергией квантово-механической формулой E = hf.

2. Если в двух точках образца фазы различны, то между этими точками должен наблюдаться поток вещества. Если разность фаз постоянна во времени, то поток также постоянен. Но если разность фаз осциллирует во времени, то и поток осциллирует.

Посмотрим, как эти свойства отражаются на поведении джозефсоновского перехода, изображённого на рис. 12-10. Между сверхпроводниками А и В по обеим сторонам диэлектрического слоя имеется напряжение U. Потенциальная энергия заряда равна величине заряда, умноженной на приложенное напряжение. Разность напряжений для куперовских пар в А и В равна U В. Поэтому энергии куперовских пар зарядом 2е в этих сверхпроводниках отличаются на величину 2еU. Это означает, что разность фаз между двумя сверхпроводниками осциллирует с частотой f = 2eU/h.

Наличие такой осциллирующей фазы в свою очередь означает, что между сверхпроводниками А и В течёт переменный ток той же частоты. Как мы знаем, переменный ток является генератором фотонов той же частоты. Именно это и наблюдается, и называется эффектом Джозефсона.

Одна сторона эффекта Джозефсона особенно поразительна. Фундаментальным следствием основных законов квантовой механики является то, что частота волновой функции определяется энергией системы. Во многих случаях, о которых шла речь выше, эта частота явно не проявляется в экспериментах. Но в эффекте Джозефсона мы можем, что называется, руками пощупать эту величину, измерив в лаборатории частоту электромагнитных волн (фотонов). Таким образом, существование эффекта Джозефсона полностью рассеивает длительные сомнения относительно реальности волновых функций и справедливости законов квантовой механики.

6. Сверхпроводники за работой

Наиболее важным практическим применением сверхпроводников до сих пор было создание электромагнитов – катушек из сверхпроводящей проволоки с током. Проволоку делают из сплава ниобия и титана. Такой материал становится сверхпроводником при температуре ниже 11 К. Сам магнит нужно охлаждать в жидком гелии при температуре 4 К, но установку конструируют так, чтобы магнитное поле было доступно в некотором объёме при комнатной температуре. Подобные магниты используются в ЯМР-установках для медицинской диагностики и в ускорителях элементарных частиц, где необходимы очень сильные магнитные поля.

До того как сверхпроводящие магниты стали практичными и доступными, использовались обычные электромагниты – железный сердечник с намотанной на него медной проволокой. Медь – хороший проводник, но всё же обладает сопротивлением. Поэтому при прохождении тока катушка нагревается: электрическая энергия превращается в тепловую. Это явление имеет два нежелательных следствия – существенные затраты электроэнергии и ограниченность создаваемого магнитного поля. Выделяемую теплоту необходимо как-то отводить, в противном случае магнит может расплавиться.

В сверхпроводящем магните проволока имеет нулевое сопротивление, поэтому электрический ток вообще её не нагревает. Критические магнитные поля в используемых сплавах очень высоки, поэтому современные сверхпроводящие магниты создают намного более сильные поля без существенных затрат энергии. Пока что это самое успешное практическое применение сверхпроводимости. Существуют предложения по использованию сверхпроводников в других областях техники. Примерами могут служить сверхпроводящие кабели для передачи электроэнергии и джозефсоновские переходы в электронных устройствах. Поиски продолжаются.

Сокр. пер. с англ. А.В.БЕРКОВА
berkov@migmail.ru